Под фракталами понимают фигуры, особенность которых — подобие самим себе. В рамках курсовой работы по C++ мы написали приложение, шустро отрисовывающее 3D-фракталы и позволяющее их вращать, приближать-отдалять, изменять параметры, записывать видео и не только. В этой статье расскажем, как шла разработка, с какими задачами в ходе неё мы сталкивались и как их решали.
Фрактал — это фигура (множество точек), подобная своей части. Такое свойство влечет за собой довольно необычные особенности. Так, фрактал нетривиален при любом масштабе, то есть в отличие от регулярных фигур (эллипсов, тетраэдров, графиков гладких функций), которые при бесконечном приближении стремятся стать фрагментом прямой, внешний вид фракталов никак не упрощается при увеличении масштаба.
Фракталы можно задавать и строить по-разному. Одни из самых простых в построении — это фрактальные кривые. Таковой, например, является снежинка Коха. Генерируется она несложной рекурсивной процедурой.
Начнем с ломаной с тремя изломами, как на картинке (n=1), и назовем её генератором. Далее каждое звено ломаной заменим на фигуру, подобную генератору, и будем продолжать так до бесконечности.
Снежинка Коха
Более интересные двухмерные фракталы можно задать, исследуя рекурсивные итерации многочлена на комплексной плоскости. Например, пусть P(z) — многочлен, а z0 — комплексное число. Тогда можно рассмотреть следующую комплексно-числовую последовательность: z0, z1=P(z0), z2=P(P(z0)), …, zn=P(zn-1), …. При стремлении n к бесконечности, такая последовательность может вести себя по-разному:
Так, например, известный фрактал — множество Жюлиа — это множество так называемых точек бифуркации для многочлена P(z)=z2+c. То есть таких значений z0, при сколь угодно малых изменениях которых поведение последовательности zn может менять тип своего поведения.
Другой пример — множество Мандельброта — это все комплексные c такие, что при P(z)=z2+c и фиксированном z0, последовательность zn не стремится к бесконечности.
Такие способы, основанные на построении рекурсивной последовательности, легко обобщаются и на трехмерные фракталы. Для этого вместо двумерных комплексных чисел нужно использовать трехмерные гиперкомплексные числа. В нашем проекте для задания фракталов мы использовали именно этот подход.
Помимо прямого трехмерного обобщения множества Мандельброта, в проекте мы добавили возможность выбора из пяти других фракталов, всё так же основывающихся на методе рекурсивной последовательности. Все они задаются уравнением zn+c (n пользователь приложения может задать сам), но для каждого из них по-своему задана операция возведения в степень трёхмерного гиперкомплексного числа z.
Призадуматься нас заставил поиск технологии графической отрисовки. Самый банальный способ что-то отрисовать — двойным вложенным циклом для каждого пикселя посчитать, какого цвета он должен быть, и покрасить. Такой подход использует ресурсы исключительно CPU, причём в одном потоке. В качестве эксперимента мы попробовали реализовать именно такой способ отрисовки даже не 3D-, а 2D-фракталов. Производительность, как нетрудно предположить, была критически низкой: на разрешении FullHD кадр рендерился больше 10 секунд. Это никуда не годилось.
Спасибо нашему ментору, который развеял наши надежды на CPU-подход и чётко направил работу в сторону рендеринга силами GPU (а ведь изначально мы рассматривали идею просто оптимизировать CPU-отрисовку). Мы остановились на OpenGL. К слову, ни у кого из членов нашей команды опыта написания GPU-шейдеров не было, поэтому пришлось изучать всё с основ.
Volume ray casting отлично подходит для рендеринга 3D-фрактала, ибо определять, не упёрлись ли мы в него, совсем нетрудно. Одной из альтернатив является технология volume ray tracing (трассировка лучей). Про её отличие от casting рассказано в той же статье. Выбор на именно casting пал по банальной причине: он в разы быстрее tracing’а, хоть и может уступать по качеству. Мы пробовали рисовать фракталы обоими способами, и трассировка, в отличие от бросания, работала неприемлемо медленно.
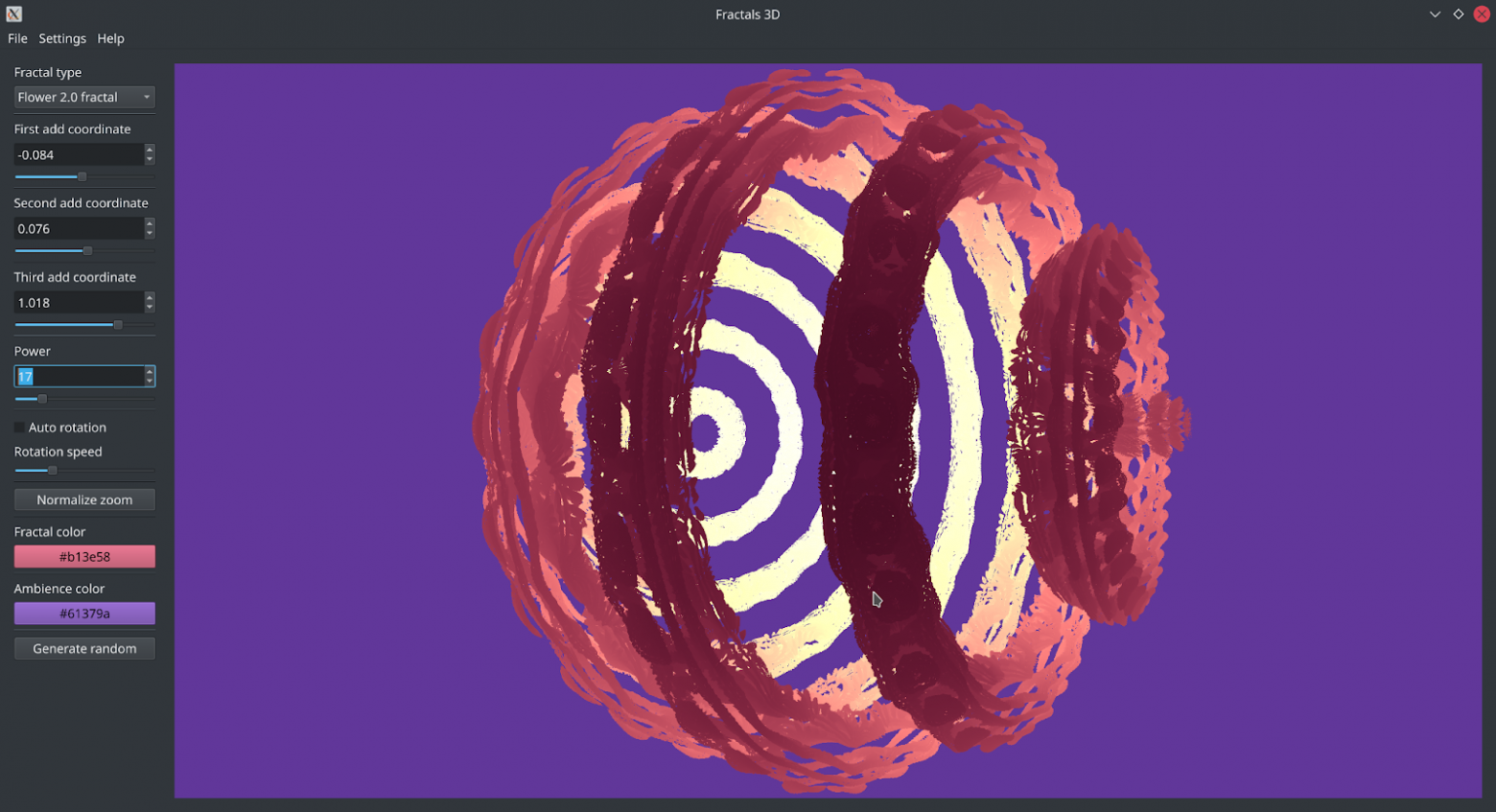
Внешний вид программы
В нашем приложении был реализован такой функционал:
1. Выбор типа и параметров фрактала. Пользователю доступны:
2. Отрисовка фрактала.
3. Вращение, приближение-отдаление при помощи мыши.
В то время как увеличение было реализовано без лишних затруднений, реализация вращения оказалась для нас нетривиальной задачей. Правильно применить матрицу поворота в шейдере получилось по итогу длительных проб и ошибок.
4. Изменение параметров фрактала «на ходу» — фрактал рендерится вместе с движением ползунков, вводом в поля новых значений параметров.
5. Кнопка генерации случайного фрактала. Здесь мы позаботились об отсеивании слишком схожих цветов фрактала и фона.
6. Автовращение.
7. Фуллскрин.
8. Возвращение масштаба и положения камеры в исходную позицию.
9. Сохранение/загрузка текущих параметров фрактала и положения камеры в/из json-файл(а).
10. Фото- и видеосъёмка фрактала:
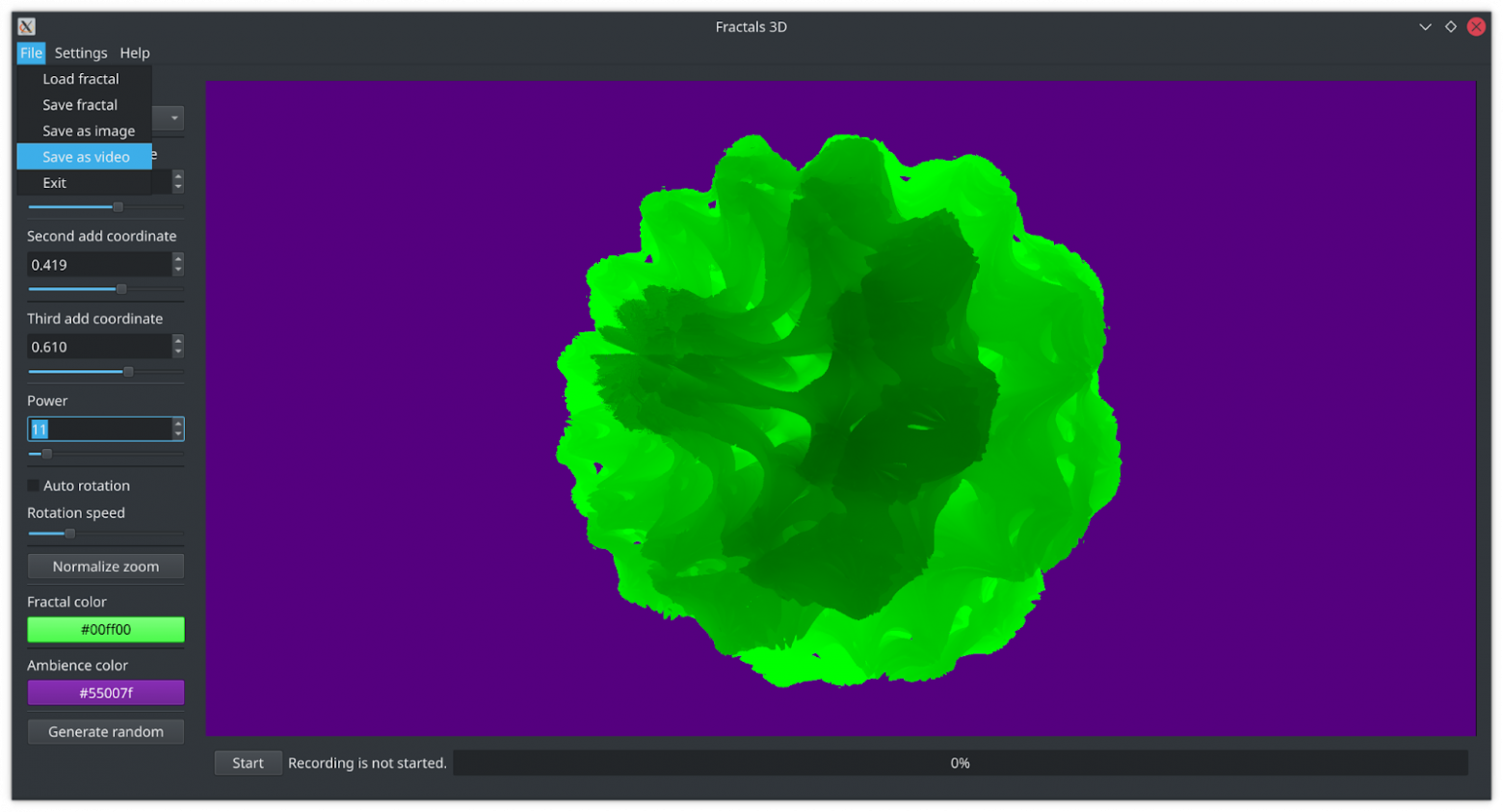В режиме записи видео
Конечно, проект далёк от завершения. Вот лишь некоторые из направлений для дальнейшей работы:
Фрактал circle
Фрактал Мандельброта
Ссылка на наш репозиторий.
habr.com
Кто мы?
Разработкой приложения в течение пяти месяцев занимались три человека: Сергей Журавлев, Степан Константинов и Дарья Леднева — все первокурсники бакалаврской программы «Прикладная математика и информатика» петербургского кампуса НИУ ВШЭ. Менторил нас Антон @0xfe0d Соснин.Задумка темы проекта
Понимая, что на первом году обучения ребята ещё слишком юны, руководство образовательной программы не требует от проектов первокурсников научной новизны. Это довольно сильно упрощает выбор идеи. Мы решили ничего не выдумывать и остановиться на нисколько не новой, но интересной теме — 3D-фракталах, ибо было понятно, что такой проект выйдет зрелищным и эффектным.Немного о фракталах
Давайте чутка разберёмся, что такое фракталы, и как они задаются.Фрактал — это фигура (множество точек), подобная своей части. Такое свойство влечет за собой довольно необычные особенности. Так, фрактал нетривиален при любом масштабе, то есть в отличие от регулярных фигур (эллипсов, тетраэдров, графиков гладких функций), которые при бесконечном приближении стремятся стать фрагментом прямой, внешний вид фракталов никак не упрощается при увеличении масштаба.
Фракталы можно задавать и строить по-разному. Одни из самых простых в построении — это фрактальные кривые. Таковой, например, является снежинка Коха. Генерируется она несложной рекурсивной процедурой.
Начнем с ломаной с тремя изломами, как на картинке (n=1), и назовем её генератором. Далее каждое звено ломаной заменим на фигуру, подобную генератору, и будем продолжать так до бесконечности.
Более интересные двухмерные фракталы можно задать, исследуя рекурсивные итерации многочлена на комплексной плоскости. Например, пусть P(z) — многочлен, а z0 — комплексное число. Тогда можно рассмотреть следующую комплексно-числовую последовательность: z0, z1=P(z0), z2=P(P(z0)), …, zn=P(zn-1), …. При стремлении n к бесконечности, такая последовательность может вести себя по-разному:
- стремиться к бесконечности;
- стремиться к какому-то конечному пределу;
- зациклиться и не иметь предела вообще.
Так, например, известный фрактал — множество Жюлиа — это множество так называемых точек бифуркации для многочлена P(z)=z2+c. То есть таких значений z0, при сколь угодно малых изменениях которых поведение последовательности zn может менять тип своего поведения.
Другой пример — множество Мандельброта — это все комплексные c такие, что при P(z)=z2+c и фиксированном z0, последовательность zn не стремится к бесконечности.
Такие способы, основанные на построении рекурсивной последовательности, легко обобщаются и на трехмерные фракталы. Для этого вместо двумерных комплексных чисел нужно использовать трехмерные гиперкомплексные числа. В нашем проекте для задания фракталов мы использовали именно этот подход.
Помимо прямого трехмерного обобщения множества Мандельброта, в проекте мы добавили возможность выбора из пяти других фракталов, всё так же основывающихся на методе рекурсивной последовательности. Все они задаются уравнением zn+c (n пользователь приложения может задать сам), но для каждого из них по-своему задана операция возведения в степень трёхмерного гиперкомплексного числа z.
Выбор технологий для UI и графики
Единственным обязательным условием, которое накладывало на курсовые работы руководство программы, было использование C++ в качестве основного языка. Ну а раз язык обязали взять классический, то и GUI библиотеку мы выбрали соответствующую — Qt.Призадуматься нас заставил поиск технологии графической отрисовки. Самый банальный способ что-то отрисовать — двойным вложенным циклом для каждого пикселя посчитать, какого цвета он должен быть, и покрасить. Такой подход использует ресурсы исключительно CPU, причём в одном потоке. В качестве эксперимента мы попробовали реализовать именно такой способ отрисовки даже не 3D-, а 2D-фракталов. Производительность, как нетрудно предположить, была критически низкой: на разрешении FullHD кадр рендерился больше 10 секунд. Это никуда не годилось.
Спасибо нашему ментору, который развеял наши надежды на CPU-подход и чётко направил работу в сторону рендеринга силами GPU (а ведь изначально мы рассматривали идею просто оптимизировать CPU-отрисовку). Мы остановились на OpenGL. К слову, ни у кого из членов нашей команды опыта написания GPU-шейдеров не было, поэтому пришлось изучать всё с основ.
О способе рендеринга фракталов
Отрисовку фракталов мы реализовали при помощи технологии volume ray casting — про неё есть хорошая статья на Хабре. Коротко о технологии: бросаем лучи в направлении от камеры и идём по ним, пока не встретим точку, принадлежащую фракталу. Так мы получаем карту его глубин, на основе чего и отрисовываем кадр. Оттенок цвета точки фрактала будем выбирать исходя количества итераций, потребовавшихся для того, чтобы дойти до этой точки (чем отдалённее — тем светлее). Разумеется, мы устанавливаем некоторый лимит на дальность проброса луча.Volume ray casting отлично подходит для рендеринга 3D-фрактала, ибо определять, не упёрлись ли мы в него, совсем нетрудно. Одной из альтернатив является технология volume ray tracing (трассировка лучей). Про её отличие от casting рассказано в той же статье. Выбор на именно casting пал по банальной причине: он в разы быстрее tracing’а, хоть и может уступать по качеству. Мы пробовали рисовать фракталы обоими способами, и трассировка, в отличие от бросания, работала неприемлемо медленно.
Реализованный функционал
В нашем приложении был реализован такой функционал:
1. Выбор типа и параметров фрактала. Пользователю доступны:
- выбор из шести типов фракталов;
- ввод значений координат константы для уравнения фрактала zn+c;
- ввод значения степени n из того же уравнения;
- выбор цветового тона фрактала и фона.
- выбор из шести типов фракталов;
- ввод значений координат константы для уравнения фрактала zn+c;
- ввод значения степени n из того же уравнения;
- выбор цветового тона фрактала и фона.
2. Отрисовка фрактала.
3. Вращение, приближение-отдаление при помощи мыши.
В то время как увеличение было реализовано без лишних затруднений, реализация вращения оказалась для нас нетривиальной задачей. Правильно применить матрицу поворота в шейдере получилось по итогу длительных проб и ошибок.
4. Изменение параметров фрактала «на ходу» — фрактал рендерится вместе с движением ползунков, вводом в поля новых значений параметров.
5. Кнопка генерации случайного фрактала. Здесь мы позаботились об отсеивании слишком схожих цветов фрактала и фона.
6. Автовращение.
7. Фуллскрин.
8. Возвращение масштаба и положения камеры в исходную позицию.
9. Сохранение/загрузка текущих параметров фрактала и положения камеры в/из json-файл(а).
10. Фото- и видеосъёмка фрактала:
- Изображение снимается при помощи встроенных возможностей Qt’ового класса QOpenGLWidget.
- Видео сцепляется при помощи ffmpeg’а из высокочастотных снимков, сделанных вышеупомянутым способом. Разумеется, съёмка ведётся в отдельном потоке.
Итоги и много фракталов
Проект однозначно вышел интересным и в меру сложным. Если задачи, связанные с графическим интерфейсом и записью видео, представляли из себя скорее техническую работу — чтение документаций и монотонное написание кода, — то разработка, связанная с самими фракталами, несла в себе весьма содержательную математику. Как уже говорилось, одной из наиболее сложных задач было обеспечение корректного вращения фрактала.Конечно, проект далёк от завершения. Вот лишь некоторые из направлений для дальнейшей работы:
- Одна из наиболее завораживающих вещей во фракталах — это перемещение и приближение камеры в ту часть, что подобна фигуре, видимой в исходном положении камеры. Однако определение такой точки и требуемого ракурса для зума в случае с трёхмерными фракталами — крайне нетривиальная задача, и за неё мы даже не брались. Тем не менее, самоподобие наших фракталов возможно наблюдать и так.
- Мы не сделали никаких метрических замеров скорости отрисовки разных конфигураций фракталов на разном железе. На данный момент все заключения о производительности были лишь умозрительными.
- Типов наших фракталов пусть и несколько, но все они объединены схожим способом построения. Разумеется, существует огромное количество других подходов к заданию 3D-фракталов, коих в нашем приложении не представлено.
- Степень детализации захардкожена несколькими константами в коде шейдера. Конечно, выбор уровня качества прорисовки должен быть предоставлен пользователю.
Ссылка на наш репозиторий.
Абстрактные 3D-фракталы всех сортов на C++
Привет, Хабр! Под фракталами понимают фигуры, особенность которых — подобие самим себе. В рамках курсовой работы по C++ мы написали приложение, шустро отрисовывающее 3D-фракталы и позволяющее их...
habr.com