С проникновением аналитики во многие сферы нашей жизни она не могла обойти стороной финансы. В этой статье рассмотрим ее применение для анализа ETF с целью их анализа, в том числе и с применением визуализиции.
1. О данных
Для анализа будем использовать данные ETF c базовой валютой USD: FXCN, FXRL, FXIT, FXUS и FXRU. Временной ряд рассмотрим за три года с 2018 по 2020 года. Само исследование проведем в Google Colaboratory.
Как обычно в начале импортируем все необходимые библиотеки для дальнейшей работы.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from google.colab import files
import warnings
warnings.filterwarnings("ignore")
Сначала необходимо получить данные. Есть несколько способов. Мы воспользовались — взяли их с Finam в формате csv. Дальше написали функцию для обработки полученных данных и при помощи concat свел их в один датафрейм.
def changeDF(df):
df['date'] = pd.to_datetime(df['<DATE>'].astype(str), dayfirst=True)
name =[x for x in globals() if globals()[x] is df][0]
df = df.drop(['<DATE>','<TIME>', '<OPEN>', '<HIGH>', '<LOW>'], axis=1)
df = df.set_index(['date'])
df.columns = [name+'_cl', name + '_vol']
return df
fxgd_change = changeDF(fxgd)
fxrl_change = changeDF(fxrl)
fxit_change = changeDF(fxit)
fxus_change = changeDF(fxus)
fxru_change = changeDF(fxru)
fxcn_change = changeDF(fxcn)
etf = pd.concat([fxgd_change, fxrl_change, fxit_change, fxus_change, fxru_change, fxcn_change], axis=1)
etf.head()
В результате получили:

Дальше проверим наш датасет на предмет наличия значений NULL
print(etf.isnull().sum())

Выбросим их, чтоб не мешали в дальнейшем расчете:
etf.dropna(inplace=True, axis=0)
Дальше имеет смысл посмотреть тип значений:
etf.dtypes

И посмотрим размер датасета:
etf.shape
В результате получили (752, 12).
Так же дальше интересно посмотреть как вели себя ETF в последние полгода. Это можно сделать при помощи функции describe:
etf[-120:].describe()

В результате видно в каких пределах в последние полгода ETF провели большую часть времени с вероятностью 75%.
После построим графики движения цены во времени за прошедшие три года.
fig, axs = plt.subplots(3, 2, figsize=(15,15))
axs[0, 0].plot(etf.index, etf['fxgd_cl'], 'tab:blue' )
axs[0, 0].set_title('FXGD')
axs[0, 1].plot(etf.index, etf['fxrl_cl'], 'tab range')
range')
axs[0, 1].set_title('FXRL')
axs[1, 0].plot(etf.index, etf['fxit_cl'], 'tab:green')
axs[1, 0].set_title('FXIT')
axs[1, 1].plot(etf.index, etf['fxus_cl'], 'tab:red')
axs[1, 1].set_title('FXUS')
axs[2, 0].plot(etf.index, etf['fxru_cl'], 'tab:grey')
axs[2, 0].set_title('FXRU')
axs[2, 1].plot(etf.index, etf['fxcn_cl'], 'tab urple')
urple')
axs[2, 1].set_title('FXCN')
for ax in axs.flat:
ax.set(xlabel='Data', ylabel='Price')
for ax in axs.flat:
ax.label_outer()

Ежедневное процентное изменение цены etf вычисляется на основе процентного изменения между ценами закрытия 2 последовательных дней. Предположим, что цена закрытия вчера составляла 500 рублей, а сегодня она закрылась по 550 рублей. Таким образом, процентное изменение составляет 10%. т. е. ((550-500) / 500)*100. Здесь нет никакой тайны!
Далее, мы введем новый столбец, обозначающий дневную доходность в цене etf. Вычислить можно с помощью встроенной функции pct_change() в python. Так же немного переставлю колонки, чтоб визуально лучше воспринималось.
etf_cl = etf[['fxgd_cl', 'fxrl_cl', 'fxit_cl', 'fxus_cl', 'fxru_cl', 'fxcn_cl']]
etf_cl_pct = etf_cl.pct_change()*100
etf_cl_pct.columns = ['fxgd_cl_pct', 'fxrl_cl_pct', 'fxit_cl_pct', 'fxus_cl_pct', 'fxru_cl_pct', 'fxcn_cl_pct']
etf_vol = etf[['fxgd_vol', 'fxrl_vol', 'fxit_vol', 'fxus_vol', 'fxru_vol', 'fxcn_vol']]
etf_new = pd.concat([etf_cl, etf_vol, etf_cl_pct], axis = 1)
etf_new.head()
 etf_new = etf_new.dropna()
etf_new = etf_new.dropna()
Представим изменение ежедневной доходности в виде графика во времени:
fig, axs = plt.subplots(3, 2, figsize=(15,15))
axs[0, 0].plot(etf_new.index, etf_new['fxgd_cl_pct'], 'tab:blue')
axs[0, 0].set_title('FXGD')
axs[0, 1].plot(etf_new.index, etf_new['fxrl_cl_pct'], 'tab range')
range')
axs[0, 1].set_title('FXRL')
axs[1, 0].plot(etf_new.index, etf_new['fxit_cl_pct'], 'tab:green')
axs[1, 0].set_title('FXIT')
axs[1, 1].plot(etf_new.index, etf_new['fxus_cl_pct'], 'tab:red')
axs[1, 1].set_title('FXUS')
axs[2, 0].plot(etf_new.index, etf_new['fxru_cl_pct'], 'tab:grey')
axs[2, 0].set_title('FXRU')
axs[2, 1].plot(etf_new.index, etf_new['fxcn_cl_pct'], 'tab urple')
urple')
axs[2, 1].set_title('FXCN')
for ax in axs.flat:
ax.set(xlabel='Data', ylabel='Price')
for ax in axs.flat:
ax.label_outer()

В течение большей части времени доходность составляет от -2% до 2% со скачками без пересечения отметки в 6% с обеих сторон. Наиболее шумной выглядит ETF FXCN.
Так же можно проверить новостные статьи за те дни, когда наблюдался резкий рост/падение цен на etf и понять чем это было обусловлено.
Построим гистограмму распределения ежедневных доходов:
import seaborn as sns
sns.set(style="darkgrid")
fig, axs = plt.subplots(3, 2, figsize=(15,15))
sns.histplot(data=etf_new['fxgd_cl_pct'], kde=True, color="orange", ax=axs[0, 0])
axs[0,0].set_xlim(-10,10)
sns.histplot(data=etf_new['fxrl_cl_pct'], kde=True, color="olive", ax=axs[0, 1])
axs[0,1].set_xlim(-10,10)
sns.histplot(data=etf_new['fxit_cl_pct'], kde=True, color="gold", ax=axs[1, 0])
axs[1,0].set_xlim(-10,10)
sns.histplot(data=etf_new['fxus_cl_pct'], kde=True, color="grey", ax=axs[1, 1])
axs[1,1].set_xlim(-10,10)
sns.histplot(data=etf_new['fxru_cl_pct'], kde=True, color="teal", ax=axs[2, 0])
axs[2,0].set_xlim(-10,10)
sns.histplot(data=etf_new['fxcn_cl_pct'], kde=True, color="brown", ax=axs[2, 1])
axs[2,1].set_xlim(-10,10)
plt.show()
 etf_new[['fxgd_cl_pct', 'fxrl_cl_pct', 'fxit_cl_pct', 'fxus_cl_pct', 'fxru_cl_pct', 'fxcn_cl_pct']].describe()
etf_new[['fxgd_cl_pct', 'fxrl_cl_pct', 'fxit_cl_pct', 'fxus_cl_pct', 'fxru_cl_pct', 'fxcn_cl_pct']].describe()

Гистограммы ежедневных доходностей центрированы вокруг среднего значения, которое для всех etf было больше нуля и говорит о положительном тренде. Видно, что доходность для всех ETF большую часть времени лежала в пределах от -2,5 до 2,5%. Наибольшую доходность показали — FXIT, а наименьшую — FXRU.
2. Анализ тренда
Затем мы добавляем новый столбец «Тренд», значения которого основаны на ежедневном процентном изменении, которое мы рассчитали выше. Дальше можно взглянуть как вели себя акции акцииETF в последние 3 года. Для этого их изменения можно визуализировать при помощи круговых диаграмм, где каждый сектор представляет процент дней, в течение которых происходил каждый тренд. Для построения будем использовать функцию groupby() со столбцом тренда.
def trend(x):
if x > -0.5 and x <= 0.5:
return 'Практически или без изменений'
elif x > 0.5 and x <= 1.5:
return 'Небольшой позитив'
elif x > -1.5 and x <= -0.5:
return 'Небольшой негатив'
elif x > 1.5 and x <= 2.5:
return 'Позитив'
elif x > -2.5 and x <= -1.5:
return 'Негатив'
elif x > 2.5 and x <= 5:
return 'Значительный позитив'
elif x > -5 and x <= -2.5:
return 'Значительный негатив'
elif x > 5:
return 'Максимальный позитив'
elif x <= -5:
return 'Максимальный негатив'
for stock in etf_trend.columns[12:]:
etf_trend["Trend_" + str(stock)] = np.zeros(etf_trend[stock].count())
etf_trend["Trend_"+ str(stock)] = etf_trend[stock].apply(lambda x:trend(x))
sns.set(style="darkgrid")
fig, axs = plt.subplots(3, 2, figsize=(20,17))
axs[0, 0].pie(etf_trend['Trend_fxgd_cl_pct'].value_counts(), labels = etf_trend['Trend_fxgd_cl_pct'].value_counts().index, autopct="%.1f%%")
axs[0, 0].set_title('FXGD')
axs[0, 1].pie(etf_trend['Trend_fxrl_cl_pct'].value_counts(), labels = etf_trend['Trend_fxrl_cl_pct'].value_counts().index, autopct="%.1f%%")
axs[0, 1].set_title('FXRL')
axs[1, 0].pie(etf_trend['Trend_fxit_cl_pct'].value_counts(), labels = etf_trend['Trend_fxit_cl_pct'].value_counts().index, autopct="%.1f%%")
axs[1, 0].set_title('FXIT')
axs[1, 1].pie(etf_trend['Trend_fxus_cl_pct'].value_counts(), labels = etf_trend['Trend_fxus_cl_pct'].value_counts().index, autopct="%.1f%%")
axs[1, 1].set_title('FXUS')
axs[2, 0].pie(etf_trend['Trend_fxru_cl_pct'].value_counts(), labels = etf_trend['Trend_fxru_cl_pct'].value_counts().index, autopct="%.1f%%")
axs[2, 0].set_title('FXRU')
axs[2, 1].pie(etf_trend['Trend_fxcn_cl_pct'].value_counts(), labels = etf_trend['Trend_fxcn_cl_pct'].value_counts().index, autopct="%.1f%%")
axs[2, 1].set_title('FXCN')
plt.show()

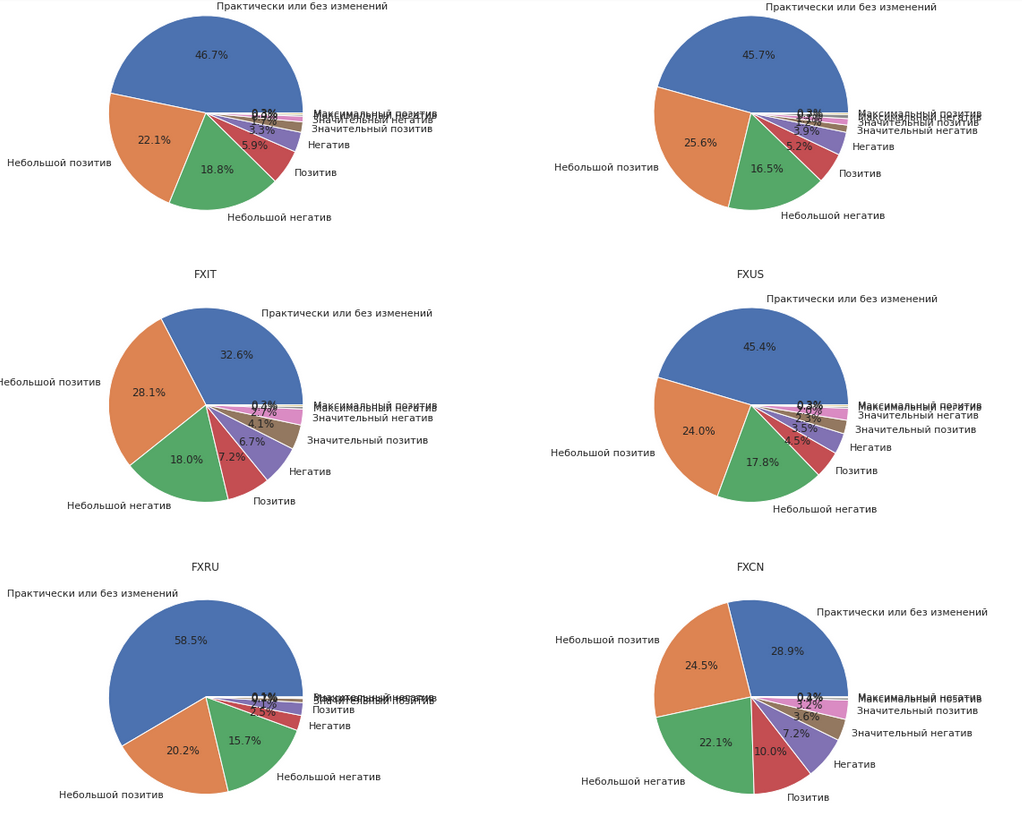
За рассматриваемый период с 2018 года по 2020 года большую часть времени ETF практически не изменялись, или изменялись незначительно при заданных параметрах. Так же важно отметить, что при небольших изменениях они как правило были позитивными. При более больших — это соотношение сохранялось кроме FXRU.
3. Ежедневная доходность и объемы
Следующим шагом продолжим работу с объемами:
sns.set(style="darkgrid")
fig, axs = plt.subplots(6, 1, figsize=(30,35))
axs[0].stem(etf_trend.index[-253:], etf_trend['fxgd_cl_pct'][-253:])
axs[0].plot((etf_trend['fxgd_vol']/10000)[-253:], color = 'green', alpha = 0.5)
axs[0].set_title('FXGD')
axs[1].stem(etf_trend.index[-253:], etf_trend['fxrl_cl_pct'][-253:])
axs[1].plot((etf_trend['fxrl_vol']/10000)[-253:], color = 'green', alpha = 0.5)
axs[1].set_title('FXRL')
axs[2].stem(etf_trend.index[-253:], etf_trend['fxit_cl_pct'][-253:])
axs[2].plot((etf_trend['fxit_vol']/10000)[-253:], color = 'green', alpha = 0.5)
axs[2].set_title('FXIT')
axs[3].stem(etf_trend.index[-253:], etf_trend['fxus_cl_pct'][-253:])
axs[3].plot((etf_trend['fxus_vol']/10000)[-253:], color = 'green', alpha = 0.5)
axs[3].set_title('FXUS')
axs[4].stem(etf_trend.index[-253:], etf_trend['fxru_cl_pct'][-253:])
axs[4].plot((etf_trend['fxru_vol']/10000)[-253:], color = 'green', alpha = 0.5)
axs[4].set_title('FXRU')
axs[5].stem(etf_trend.index[-253:], etf_trend['fxcn_cl_pct'][-253:])
axs[5].plot((etf_trend['fxcn_vol']/10000)[-253:], color = 'green', alpha = 0.5)
axs[5].set_title('FXCN')
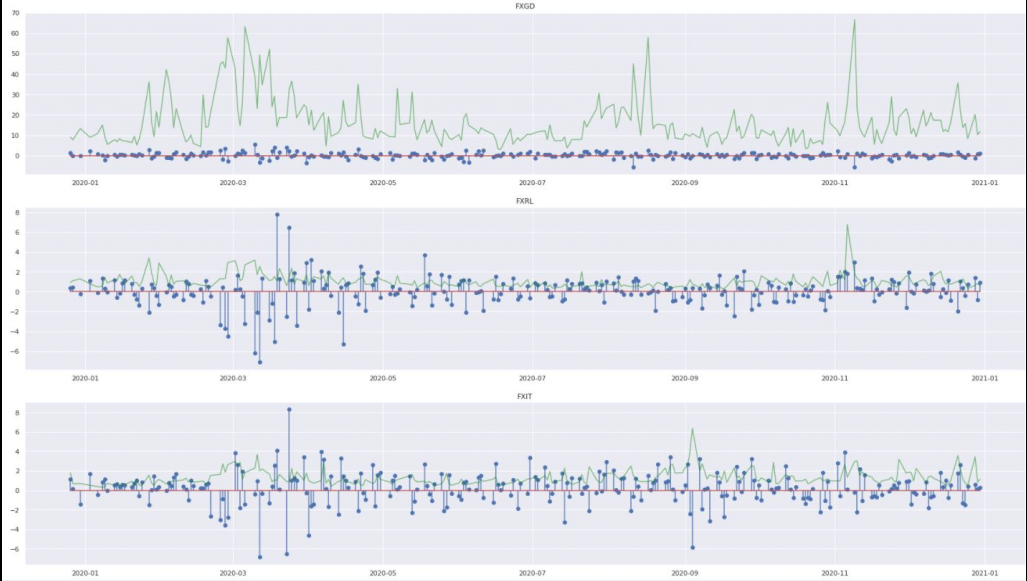

Сопоставляя ежедневный объем торговли(зеленым цветом) с ежедневной доходностью(синим цветом), было отмечено, что часто для ETF характерно, что когда объем торгов высок, наблюдается сравнительно высокий рост или падение цены. Объем торгов ETF в сочетании с ростом или падениемы на данный инструмент является показателем доверия трейдеров и инвесторов к конкретному ETF.
4. Корреляционный анализ ETF
Основное правило диверсификации — не клади все яйца в одну корзинку. По этому если мы решили собирать портфель из ETF, то они не должны быть сильно взаимосвязаны друг с другом. Математическим языком — коэффициент корреляции Пирсона между любой парой должен быть близок к 0. Смысл — они не должны падать синхронно, чтоб инвестиции не превратились в 0.
Проанализировать корреляцию между различными ETF можно с помощью парной диаграммы Seaborn. Для удобства оставим только процентные изменения за день в отдельном новом датафрейме.
pct_chg_etf = etf_new[etf_new.columns[12:]]
sns.set(style = 'ticks', font_scale = 1.25)
sns.pairplot(pct_chg_etf)
plt.show()

На графике визуально можно увидеть наличие корреляции между различными ETF. Обратите внимание, что корреляционный анализ выполняется для ежедневного процентного изменения(дневной доходности) цены ETF, а не для их цены.
Из полученных графиков ясно видно, что следующие FXIT и FXUS не следует класть в одну корзину, так как между нми наблюдается сильная зависимость. Остальные могут быть включены в портфель, поскольку ни одна из двух оставшихся ETF не демонстрирует какой-либо существенной корреляции.
Но у визуального анализа есть существенный недостаток — он не предоставляет подробной информации о количественной оценки взаимосвязи, таких как значение R Пирсона и p нулевой гипотезы. В связи с чем при визуальном анализе остается под вопросом FXCN — есть ли у данного ETF сильная взаимосвязь с FXUS или нет.
Один из способов решения данного вопроса — построение графиков seaborn.jointplot с подробной информацией по значению R Пирсона (коэффициент корреляции Пирсона) для каждой пары ETF. Значение R Пирсона колеблется от -1 до 1. Отрицательное значение указывает на отрицательную линейную связь, в то время как положительное значение указывает на положительную связь. Значение R Пирсона ближе к 1 (или -1) указывает на сильную корреляцию, в то время как значение ближе к 0 указывает на слабую корреляцию.
Так же чем интересны данные графики — построение гистограмм распределения по краям, а так же значение p-value.
Но если рассматривать все пары, то нам потребуется большое количество графиков. По этому остановимся только на тех, которые вызывают сомнения:
from scipy.stats import stats
a_1 = pct_chg_etf.fxit_cl_pct
b_1 = pct_chg_etf.fxus_cl_pct
b_2 = pct_chg_etf.fxcn_cl_pct
g_1 = sns.jointplot('fxit_cl_pct', 'fxcn_cl_pct', pct_chg_etf, kind = 'scatter')
r_1, p_1 = stats.pearsonr(a_1, b_1)
g_1.ax_joint.annotate(f'$\\rho = {r_1:.3f}, p = {p_1:.3f}$',
xy=(0.1, 0.9), xycoords='axes fraction',
ha='left', va='center',
bbox={'boxstyle': 'round', 'fc': 'powderblue', 'ec': 'navy'})
g_1.ax_joint.scatter(a_1, b_1)
g_1.set_axis_labels(xlabel='fxit', ylabel='fxus', size=15)
g_2 = sns.jointplot('fxus_cl_pct', 'fxit_cl_pct', pct_chg_etf, kind = 'scatter')
r_2, p_2 = stats.pearsonr(a_1, b_2)
g_2.ax_joint.annotate(f'$\\rho = {r_2:.3f}, p = {p_2:.3f}$',
xy=(0.1, 0.9), xycoords='axes fraction',
ha='left', va='center',
bbox={'boxstyle': 'round', 'fc': 'powderblue', 'ec': 'navy'})
g_2.ax_joint.scatter(a_1, b_2)
g_2.set_axis_labels(xlabel='fxit', ylabel='fxcn', size=15)
plt.tight_layout()
plt.show()

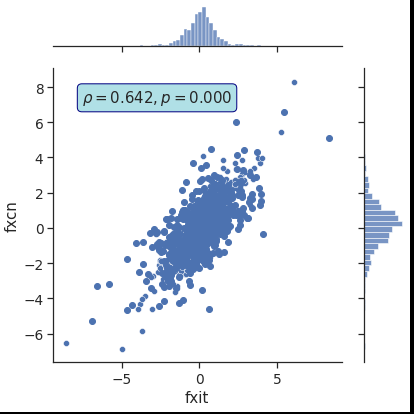
Первый график подтвердил наличие сильной взаимосвязи между FXIT и FXUS, что говорит о нежелательности их брать в один портфель. В свою очередь корреляция между FXCN и FXIT оказалась ниже 0,7, что говорит о возможности совместного нахождения в одной корзине.
5. Анализ волатильности
Волатильность-один из важнейших показателей на финансовых рынках. Говорят, что ценная бумага обладает высокой волатильностью, если ее стоимость может резко измениться за короткий промежуток времени. С другой стороны, более низкая волатильность означает, что стоимость имеет тенденцию быть относительно стабильной в течение определенного периода времени. Эти изменения обусловлены несколькими факторами, включая спрос и предложение, настроения, жадность, страх и т.д. Математически волатильность измеряется с помощью статистической меры, называемой «стандартным отклонением», которая измеряет отклонение актива от его средней стоимости.
Произведем расчет 5-дневной скользящей средней дневной доходности и стандартного отклонения. После этого построим график. Все это можно выполнить при помощи функций Pandas rolling() и std().
sns.set(style="darkgrid")
fig, axs = plt.subplots(6, 1, figsize=(30,35))
for i, etf in enumerate(pct_chg_etf.columns):
axs.plot(pct_chg_etf[etf].rolling(5).std()*np.sqrt(5))
axs.plot(pct_chg_etf[etf].rolling(7).mean())
axs.set_title(etf[:4], size=20)
 volatility = pct_chg_etf[['fxgd_cl_pct', 'fxrl_cl_pct', 'fxit_cl_pct', 'fxus_cl_pct','fxru_cl_pct', 'fxcn_cl_pct']].rolling(5).std()*np.sqrt(5)
volatility = pct_chg_etf[['fxgd_cl_pct', 'fxrl_cl_pct', 'fxit_cl_pct', 'fxus_cl_pct','fxru_cl_pct', 'fxcn_cl_pct']].rolling(5).std()*np.sqrt(5)
volatility[:150].plot(linewidth=4, figsize = (35, 15))
plt.legend(loc=2, prop={'size': 16})

Как результат вы можете заметить, что наиболее сильная низкая волатильность характерна для ETF на российские еврооблигации — FXRU.
Многие трейдеры и инвесторы ищут инвестиции с более высокой волатильностью, чтобы получать более высокую прибыль. Если финансовый инструмент не движется, он не только обладает низкой волатильностью, но и имеет низкий потенциал прибыли. С другой стороны, ценные бумаги с очень высоким уровнем волатильности могут иметь огромный потенциал прибыли, но риск также высок.
 habr.com
habr.com
1. О данных
Для анализа будем использовать данные ETF c базовой валютой USD: FXCN, FXRL, FXIT, FXUS и FXRU. Временной ряд рассмотрим за три года с 2018 по 2020 года. Само исследование проведем в Google Colaboratory.
Как обычно в начале импортируем все необходимые библиотеки для дальнейшей работы.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from google.colab import files
import warnings
warnings.filterwarnings("ignore")
Сначала необходимо получить данные. Есть несколько способов. Мы воспользовались — взяли их с Finam в формате csv. Дальше написали функцию для обработки полученных данных и при помощи concat свел их в один датафрейм.
def changeDF(df):
df['date'] = pd.to_datetime(df['<DATE>'].astype(str), dayfirst=True)
name =[x for x in globals() if globals()[x] is df][0]
df = df.drop(['<DATE>','<TIME>', '<OPEN>', '<HIGH>', '<LOW>'], axis=1)
df = df.set_index(['date'])
df.columns = [name+'_cl', name + '_vol']
return df
fxgd_change = changeDF(fxgd)
fxrl_change = changeDF(fxrl)
fxit_change = changeDF(fxit)
fxus_change = changeDF(fxus)
fxru_change = changeDF(fxru)
fxcn_change = changeDF(fxcn)
etf = pd.concat([fxgd_change, fxrl_change, fxit_change, fxus_change, fxru_change, fxcn_change], axis=1)
etf.head()
В результате получили:

Дальше проверим наш датасет на предмет наличия значений NULL
print(etf.isnull().sum())

Выбросим их, чтоб не мешали в дальнейшем расчете:
etf.dropna(inplace=True, axis=0)
Дальше имеет смысл посмотреть тип значений:
etf.dtypes

И посмотрим размер датасета:
etf.shape
В результате получили (752, 12).
Так же дальше интересно посмотреть как вели себя ETF в последние полгода. Это можно сделать при помощи функции describe:
etf[-120:].describe()

В результате видно в каких пределах в последние полгода ETF провели большую часть времени с вероятностью 75%.
После построим графики движения цены во времени за прошедшие три года.
fig, axs = plt.subplots(3, 2, figsize=(15,15))
axs[0, 0].plot(etf.index, etf['fxgd_cl'], 'tab:blue' )
axs[0, 0].set_title('FXGD')
axs[0, 1].plot(etf.index, etf['fxrl_cl'], 'tab
axs[0, 1].set_title('FXRL')
axs[1, 0].plot(etf.index, etf['fxit_cl'], 'tab:green')
axs[1, 0].set_title('FXIT')
axs[1, 1].plot(etf.index, etf['fxus_cl'], 'tab:red')
axs[1, 1].set_title('FXUS')
axs[2, 0].plot(etf.index, etf['fxru_cl'], 'tab:grey')
axs[2, 0].set_title('FXRU')
axs[2, 1].plot(etf.index, etf['fxcn_cl'], 'tab
axs[2, 1].set_title('FXCN')
for ax in axs.flat:
ax.set(xlabel='Data', ylabel='Price')
for ax in axs.flat:
ax.label_outer()

Ежедневное процентное изменение цены etf вычисляется на основе процентного изменения между ценами закрытия 2 последовательных дней. Предположим, что цена закрытия вчера составляла 500 рублей, а сегодня она закрылась по 550 рублей. Таким образом, процентное изменение составляет 10%. т. е. ((550-500) / 500)*100. Здесь нет никакой тайны!
Далее, мы введем новый столбец, обозначающий дневную доходность в цене etf. Вычислить можно с помощью встроенной функции pct_change() в python. Так же немного переставлю колонки, чтоб визуально лучше воспринималось.
etf_cl = etf[['fxgd_cl', 'fxrl_cl', 'fxit_cl', 'fxus_cl', 'fxru_cl', 'fxcn_cl']]
etf_cl_pct = etf_cl.pct_change()*100
etf_cl_pct.columns = ['fxgd_cl_pct', 'fxrl_cl_pct', 'fxit_cl_pct', 'fxus_cl_pct', 'fxru_cl_pct', 'fxcn_cl_pct']
etf_vol = etf[['fxgd_vol', 'fxrl_vol', 'fxit_vol', 'fxus_vol', 'fxru_vol', 'fxcn_vol']]
etf_new = pd.concat([etf_cl, etf_vol, etf_cl_pct], axis = 1)
etf_new.head()

Представим изменение ежедневной доходности в виде графика во времени:
fig, axs = plt.subplots(3, 2, figsize=(15,15))
axs[0, 0].plot(etf_new.index, etf_new['fxgd_cl_pct'], 'tab:blue')
axs[0, 0].set_title('FXGD')
axs[0, 1].plot(etf_new.index, etf_new['fxrl_cl_pct'], 'tab
axs[0, 1].set_title('FXRL')
axs[1, 0].plot(etf_new.index, etf_new['fxit_cl_pct'], 'tab:green')
axs[1, 0].set_title('FXIT')
axs[1, 1].plot(etf_new.index, etf_new['fxus_cl_pct'], 'tab:red')
axs[1, 1].set_title('FXUS')
axs[2, 0].plot(etf_new.index, etf_new['fxru_cl_pct'], 'tab:grey')
axs[2, 0].set_title('FXRU')
axs[2, 1].plot(etf_new.index, etf_new['fxcn_cl_pct'], 'tab
axs[2, 1].set_title('FXCN')
for ax in axs.flat:
ax.set(xlabel='Data', ylabel='Price')
for ax in axs.flat:
ax.label_outer()

В течение большей части времени доходность составляет от -2% до 2% со скачками без пересечения отметки в 6% с обеих сторон. Наиболее шумной выглядит ETF FXCN.
Так же можно проверить новостные статьи за те дни, когда наблюдался резкий рост/падение цен на etf и понять чем это было обусловлено.
Построим гистограмму распределения ежедневных доходов:
import seaborn as sns
sns.set(style="darkgrid")
fig, axs = plt.subplots(3, 2, figsize=(15,15))
sns.histplot(data=etf_new['fxgd_cl_pct'], kde=True, color="orange", ax=axs[0, 0])
axs[0,0].set_xlim(-10,10)
sns.histplot(data=etf_new['fxrl_cl_pct'], kde=True, color="olive", ax=axs[0, 1])
axs[0,1].set_xlim(-10,10)
sns.histplot(data=etf_new['fxit_cl_pct'], kde=True, color="gold", ax=axs[1, 0])
axs[1,0].set_xlim(-10,10)
sns.histplot(data=etf_new['fxus_cl_pct'], kde=True, color="grey", ax=axs[1, 1])
axs[1,1].set_xlim(-10,10)
sns.histplot(data=etf_new['fxru_cl_pct'], kde=True, color="teal", ax=axs[2, 0])
axs[2,0].set_xlim(-10,10)
sns.histplot(data=etf_new['fxcn_cl_pct'], kde=True, color="brown", ax=axs[2, 1])
axs[2,1].set_xlim(-10,10)
plt.show()


Гистограммы ежедневных доходностей центрированы вокруг среднего значения, которое для всех etf было больше нуля и говорит о положительном тренде. Видно, что доходность для всех ETF большую часть времени лежала в пределах от -2,5 до 2,5%. Наибольшую доходность показали — FXIT, а наименьшую — FXRU.
2. Анализ тренда
Затем мы добавляем новый столбец «Тренд», значения которого основаны на ежедневном процентном изменении, которое мы рассчитали выше. Дальше можно взглянуть как вели себя акции акцииETF в последние 3 года. Для этого их изменения можно визуализировать при помощи круговых диаграмм, где каждый сектор представляет процент дней, в течение которых происходил каждый тренд. Для построения будем использовать функцию groupby() со столбцом тренда.
def trend(x):
if x > -0.5 and x <= 0.5:
return 'Практически или без изменений'
elif x > 0.5 and x <= 1.5:
return 'Небольшой позитив'
elif x > -1.5 and x <= -0.5:
return 'Небольшой негатив'
elif x > 1.5 and x <= 2.5:
return 'Позитив'
elif x > -2.5 and x <= -1.5:
return 'Негатив'
elif x > 2.5 and x <= 5:
return 'Значительный позитив'
elif x > -5 and x <= -2.5:
return 'Значительный негатив'
elif x > 5:
return 'Максимальный позитив'
elif x <= -5:
return 'Максимальный негатив'
for stock in etf_trend.columns[12:]:
etf_trend["Trend_" + str(stock)] = np.zeros(etf_trend[stock].count())
etf_trend["Trend_"+ str(stock)] = etf_trend[stock].apply(lambda x:trend(x))
sns.set(style="darkgrid")
fig, axs = plt.subplots(3, 2, figsize=(20,17))
axs[0, 0].pie(etf_trend['Trend_fxgd_cl_pct'].value_counts(), labels = etf_trend['Trend_fxgd_cl_pct'].value_counts().index, autopct="%.1f%%")
axs[0, 0].set_title('FXGD')
axs[0, 1].pie(etf_trend['Trend_fxrl_cl_pct'].value_counts(), labels = etf_trend['Trend_fxrl_cl_pct'].value_counts().index, autopct="%.1f%%")
axs[0, 1].set_title('FXRL')
axs[1, 0].pie(etf_trend['Trend_fxit_cl_pct'].value_counts(), labels = etf_trend['Trend_fxit_cl_pct'].value_counts().index, autopct="%.1f%%")
axs[1, 0].set_title('FXIT')
axs[1, 1].pie(etf_trend['Trend_fxus_cl_pct'].value_counts(), labels = etf_trend['Trend_fxus_cl_pct'].value_counts().index, autopct="%.1f%%")
axs[1, 1].set_title('FXUS')
axs[2, 0].pie(etf_trend['Trend_fxru_cl_pct'].value_counts(), labels = etf_trend['Trend_fxru_cl_pct'].value_counts().index, autopct="%.1f%%")
axs[2, 0].set_title('FXRU')
axs[2, 1].pie(etf_trend['Trend_fxcn_cl_pct'].value_counts(), labels = etf_trend['Trend_fxcn_cl_pct'].value_counts().index, autopct="%.1f%%")
axs[2, 1].set_title('FXCN')
plt.show()

За рассматриваемый период с 2018 года по 2020 года большую часть времени ETF практически не изменялись, или изменялись незначительно при заданных параметрах. Так же важно отметить, что при небольших изменениях они как правило были позитивными. При более больших — это соотношение сохранялось кроме FXRU.
3. Ежедневная доходность и объемы
Следующим шагом продолжим работу с объемами:
sns.set(style="darkgrid")
fig, axs = plt.subplots(6, 1, figsize=(30,35))
axs[0].stem(etf_trend.index[-253:], etf_trend['fxgd_cl_pct'][-253:])
axs[0].plot((etf_trend['fxgd_vol']/10000)[-253:], color = 'green', alpha = 0.5)
axs[0].set_title('FXGD')
axs[1].stem(etf_trend.index[-253:], etf_trend['fxrl_cl_pct'][-253:])
axs[1].plot((etf_trend['fxrl_vol']/10000)[-253:], color = 'green', alpha = 0.5)
axs[1].set_title('FXRL')
axs[2].stem(etf_trend.index[-253:], etf_trend['fxit_cl_pct'][-253:])
axs[2].plot((etf_trend['fxit_vol']/10000)[-253:], color = 'green', alpha = 0.5)
axs[2].set_title('FXIT')
axs[3].stem(etf_trend.index[-253:], etf_trend['fxus_cl_pct'][-253:])
axs[3].plot((etf_trend['fxus_vol']/10000)[-253:], color = 'green', alpha = 0.5)
axs[3].set_title('FXUS')
axs[4].stem(etf_trend.index[-253:], etf_trend['fxru_cl_pct'][-253:])
axs[4].plot((etf_trend['fxru_vol']/10000)[-253:], color = 'green', alpha = 0.5)
axs[4].set_title('FXRU')
axs[5].stem(etf_trend.index[-253:], etf_trend['fxcn_cl_pct'][-253:])
axs[5].plot((etf_trend['fxcn_vol']/10000)[-253:], color = 'green', alpha = 0.5)
axs[5].set_title('FXCN')


Сопоставляя ежедневный объем торговли(зеленым цветом) с ежедневной доходностью(синим цветом), было отмечено, что часто для ETF характерно, что когда объем торгов высок, наблюдается сравнительно высокий рост или падение цены. Объем торгов ETF в сочетании с ростом или падениемы на данный инструмент является показателем доверия трейдеров и инвесторов к конкретному ETF.
4. Корреляционный анализ ETF
Основное правило диверсификации — не клади все яйца в одну корзинку. По этому если мы решили собирать портфель из ETF, то они не должны быть сильно взаимосвязаны друг с другом. Математическим языком — коэффициент корреляции Пирсона между любой парой должен быть близок к 0. Смысл — они не должны падать синхронно, чтоб инвестиции не превратились в 0.
Проанализировать корреляцию между различными ETF можно с помощью парной диаграммы Seaborn. Для удобства оставим только процентные изменения за день в отдельном новом датафрейме.
pct_chg_etf = etf_new[etf_new.columns[12:]]
sns.set(style = 'ticks', font_scale = 1.25)
sns.pairplot(pct_chg_etf)
plt.show()

На графике визуально можно увидеть наличие корреляции между различными ETF. Обратите внимание, что корреляционный анализ выполняется для ежедневного процентного изменения(дневной доходности) цены ETF, а не для их цены.
Из полученных графиков ясно видно, что следующие FXIT и FXUS не следует класть в одну корзину, так как между нми наблюдается сильная зависимость. Остальные могут быть включены в портфель, поскольку ни одна из двух оставшихся ETF не демонстрирует какой-либо существенной корреляции.
Но у визуального анализа есть существенный недостаток — он не предоставляет подробной информации о количественной оценки взаимосвязи, таких как значение R Пирсона и p нулевой гипотезы. В связи с чем при визуальном анализе остается под вопросом FXCN — есть ли у данного ETF сильная взаимосвязь с FXUS или нет.
Один из способов решения данного вопроса — построение графиков seaborn.jointplot с подробной информацией по значению R Пирсона (коэффициент корреляции Пирсона) для каждой пары ETF. Значение R Пирсона колеблется от -1 до 1. Отрицательное значение указывает на отрицательную линейную связь, в то время как положительное значение указывает на положительную связь. Значение R Пирсона ближе к 1 (или -1) указывает на сильную корреляцию, в то время как значение ближе к 0 указывает на слабую корреляцию.
Так же чем интересны данные графики — построение гистограмм распределения по краям, а так же значение p-value.
Но если рассматривать все пары, то нам потребуется большое количество графиков. По этому остановимся только на тех, которые вызывают сомнения:
from scipy.stats import stats
a_1 = pct_chg_etf.fxit_cl_pct
b_1 = pct_chg_etf.fxus_cl_pct
b_2 = pct_chg_etf.fxcn_cl_pct
g_1 = sns.jointplot('fxit_cl_pct', 'fxcn_cl_pct', pct_chg_etf, kind = 'scatter')
r_1, p_1 = stats.pearsonr(a_1, b_1)
g_1.ax_joint.annotate(f'$\\rho = {r_1:.3f}, p = {p_1:.3f}$',
xy=(0.1, 0.9), xycoords='axes fraction',
ha='left', va='center',
bbox={'boxstyle': 'round', 'fc': 'powderblue', 'ec': 'navy'})
g_1.ax_joint.scatter(a_1, b_1)
g_1.set_axis_labels(xlabel='fxit', ylabel='fxus', size=15)
g_2 = sns.jointplot('fxus_cl_pct', 'fxit_cl_pct', pct_chg_etf, kind = 'scatter')
r_2, p_2 = stats.pearsonr(a_1, b_2)
g_2.ax_joint.annotate(f'$\\rho = {r_2:.3f}, p = {p_2:.3f}$',
xy=(0.1, 0.9), xycoords='axes fraction',
ha='left', va='center',
bbox={'boxstyle': 'round', 'fc': 'powderblue', 'ec': 'navy'})
g_2.ax_joint.scatter(a_1, b_2)
g_2.set_axis_labels(xlabel='fxit', ylabel='fxcn', size=15)
plt.tight_layout()
plt.show()


Первый график подтвердил наличие сильной взаимосвязи между FXIT и FXUS, что говорит о нежелательности их брать в один портфель. В свою очередь корреляция между FXCN и FXIT оказалась ниже 0,7, что говорит о возможности совместного нахождения в одной корзине.
5. Анализ волатильности
Волатильность-один из важнейших показателей на финансовых рынках. Говорят, что ценная бумага обладает высокой волатильностью, если ее стоимость может резко измениться за короткий промежуток времени. С другой стороны, более низкая волатильность означает, что стоимость имеет тенденцию быть относительно стабильной в течение определенного периода времени. Эти изменения обусловлены несколькими факторами, включая спрос и предложение, настроения, жадность, страх и т.д. Математически волатильность измеряется с помощью статистической меры, называемой «стандартным отклонением», которая измеряет отклонение актива от его средней стоимости.
Произведем расчет 5-дневной скользящей средней дневной доходности и стандартного отклонения. После этого построим график. Все это можно выполнить при помощи функций Pandas rolling() и std().
sns.set(style="darkgrid")
fig, axs = plt.subplots(6, 1, figsize=(30,35))
for i, etf in enumerate(pct_chg_etf.columns):
axs.plot(pct_chg_etf[etf].rolling(5).std()*np.sqrt(5))
axs.plot(pct_chg_etf[etf].rolling(7).mean())
axs.set_title(etf[:4], size=20)

volatility[:150].plot(linewidth=4, figsize = (35, 15))
plt.legend(loc=2, prop={'size': 16})

Как результат вы можете заметить, что наиболее сильная низкая волатильность характерна для ETF на российские еврооблигации — FXRU.
Многие трейдеры и инвесторы ищут инвестиции с более высокой волатильностью, чтобы получать более высокую прибыль. Если финансовый инструмент не движется, он не только обладает низкой волатильностью, но и имеет низкий потенциал прибыли. С другой стороны, ценные бумаги с очень высоким уровнем волатильности могут иметь огромный потенциал прибыли, но риск также высок.

Анализ и визуализация данных в финансах — анализ ETF с использованием Python
С проникновением аналитики во многие сферы нашей жизни она не могла обойти стороной финансы. В этой статье рассмотрим ее применение для анализа ETF с целью их анализа, в том числе и с применением...
