Уравнение Шрёдингера
В 1926 году Эрвин Шрёдингер вывел знаменитое волновое уравнение, связывающее энергию системы с её волновыми свойствами. Его применение к атому водорода довольно сложно, поэтому сначала воспользуемся волновым уравнением, чтобы решить задачу о «частице в коробке». Выраженное в одномерном пространстве волновое уравнение Шрёдингера имеет вид: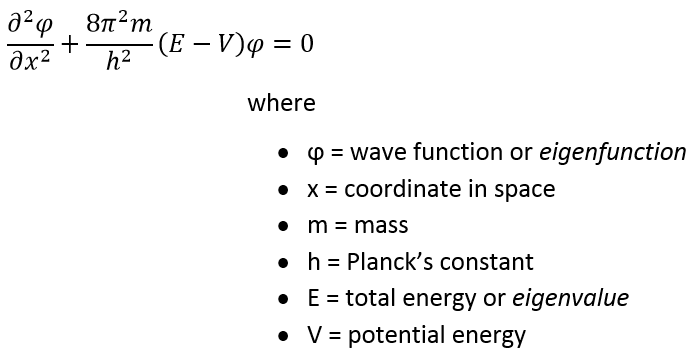
Визуализация частицы в коробке
Теперь для упрощения мы предположим о частице в коробке, что: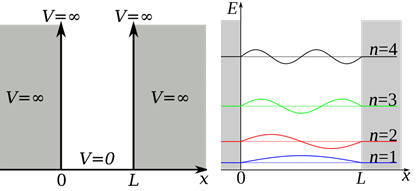
Задача о «частице в коробке» не соответствует ни одной реальной химической системе. Её полезность в контексте ситуации заключается в иллюстрировании нескольких квантово-механических особенностей. Потенциальная энергия на барьере по условию бесконечна (т. е. частица не может вырваться), а потенциальная энергия внутри коробки равна 0. В этих условиях классическая механика предсказывает, что частица имеет равную вероятность оказаться в любой точке коробки, а кинетическая энергия частицы может оказаться любой. Принимая во внимание это предположение, мы получаем различные уравнения энергии частицы у барьера и внутри коробки. На барьере V бесконечно, и, следовательно, частица не существует:
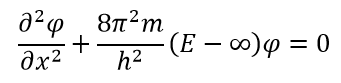
Внутри коробки V равно нулю, и, следовательно, волна может иметь любое конечное значение:
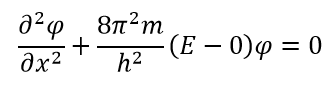
Уравнение условий внутри коробки можно переписать так:
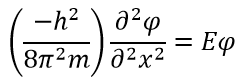
Выше видно, что волновая функция окажется такой, что при двойном дифференцировании получится та же функция, умноженная на E. Таким поведением обладает функция синуса:
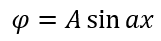
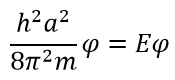
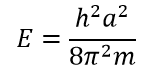
Теперь нужно вычислить значения констант α и A. В случае воспользуемся волновыми уравнениями на барьерах, где волновые функции равны 0.
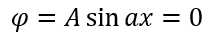
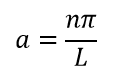
Подставляем значение для α:
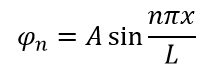
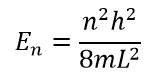
Требуя нормализации волновой функции можно определить значение A. Это утверждение верно потому, что частица должна существовать где-то в коробке. Следовательно, сумма вероятностей нахождения частицы в коробке равна 1:
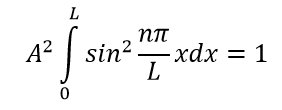
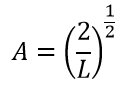
Подставляя значения, получаем окончательные уравнения волны и энергии:
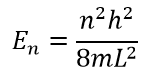
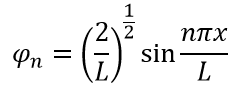
Визуализируем энергию и волновые функций при помощи Python:
import matplotlib.pyplot as plt
import numpy as np
#Constants
h = 6.626e-34
m = 9.11e-31
#Values for L and x
x_list = np.linspace(0,1,100)
L = 1
def psi(n,L,x):
return np.sqrt(2/L)*np.sin(n*np.pi*x/L)
def psi_2(n,L,x):
return np.square(psi(n,L,x))
plt.figure(figsize=(15,10))
plt.suptitle("Wave Functions", fontsize=18)
for n in range(1,4):
#Empty lists for energy and psi wave
psi_2_list = []
psi_list = []
for x in x_list:
psi_2_list.append(psi_2(n,L,x))
psi_list.append(psi(n,L,x))
plt.subplot(3,2,2*n-1)
plt.plot(x_list, psi_list)
plt.xlabel("L", fontsize=13)
plt.ylabel("Ψ", fontsize=13)
plt.xticks(np.arange(0, 1, step=0.5))
plt.title("n="+str
plt.grid()
plt.subplot(3,2,2*n)
plt.plot(x_list, psi_2_list)
plt.xlabel("L", fontsize=13)
plt.ylabel("Ψ*Ψ", fontsize=13)
plt.xticks(np.arange(0, 1, step=0.5))
plt.title("n="+str
plt.grid()
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
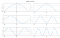
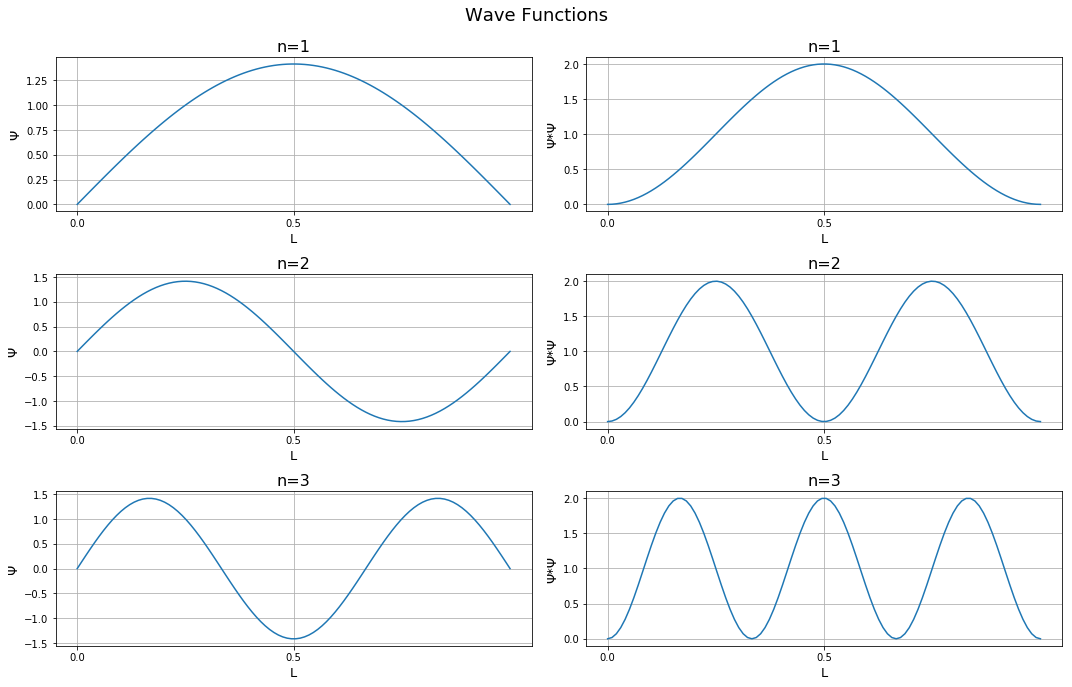
Обратите внимание, что есть области, где одновременно Ψ и Ψ * Ψ равны нулю. Они известны как узлы. Уровни энергии орбиталей не являются непрерывными. Они существуют на разных уровнях, что демонстрируется их расположением. Кроме того, с увеличением значения n плотность волны внутри коробки также увеличивается.
Визуализация орбиталей
Теперь, чтобы получить волновое уравнение относительно квантовых чисел, мы должны привести его в следующий трёхмерный формат: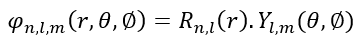
Разделение переменных зависит от типа атома, и для данной статьи оно слишком сложно. Вместо этого просто запишем решение непосредственно для построения графика. Далее воспользуемся функциями R и Y для атома водорода, не выводя их. Сначала рассмотрим орбиталь 1s:
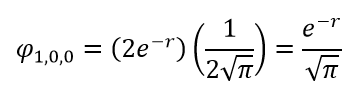
Волновая функция 1s-орбитали показывает, что вероятность появления электрона по мере удаления от ядра экспоненциально уменьшается. Она также демонстрирует сферическую форму орбитали.
import matplotlib.pyplot as plt
import numpy as np
#Probability of 1s
def prob_1s(x,y,z):
r=np.sqrt(np.square(x)+np.square
#Remember.. probability is psi squared!
return np.square(np.exp(-r)/np.sqrt(np.pi))
#Random coordinates
x=np.linspace(0,1,30)
y=np.linspace(0,1,30)
z=np.linspace(0,1,30)
elements = []
probability = []
for ix in x:
for iy in y:
for iz in z:
#Serialize into 1D object
elements.append(str((ix,iy,iz)))
probability.append(prob_1s(ix,iy,iz))
#Ensure sum of probability is 1
probability = probability/sum(probability)
#Getting electron coordinates based on probabiliy
coord = np.random.choice(elements, size=100000, replace=True, p=probability)
elem_mat = [i.split(',') for i in coord]
elem_mat = np.matrix(elem_mat)
x_coords = [float(i.item()[1:]) for i in elem_mat[:,0]]
y_coords = [float(i.item()) for i in elem_mat[:,1]]
z_coords = [float(i.item()[0:-1]) for i in elem_mat[:,2]]
#Plotting
fig = plt.figure(figsize=(10,10))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x_coords, y_coords, z_coords, alpha=0.05, s=2)
ax.set_title("Hydrogen 1s density")
plt.show()
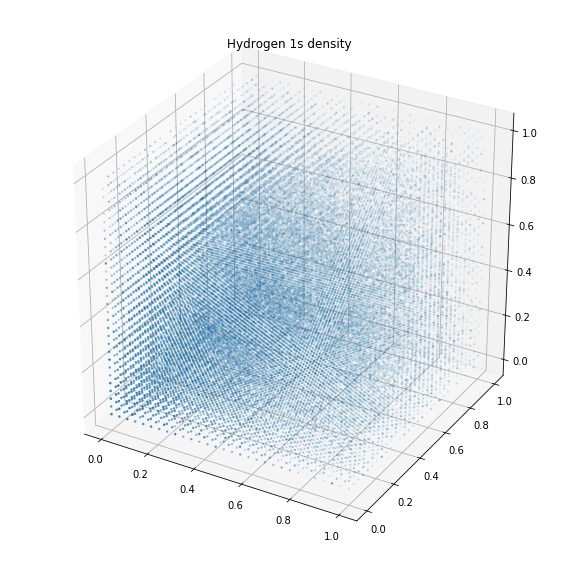
Разглядеть её на графике электронной плотности выше немного затруднительно, однако сферу в целом увидеть возможно. Плотность уменьшается по мере удаления от центра. Как правило, точкой отсчёта является момент, когда вероятность появления электрона составляет 99 %. Такие же графики плотности возможно получить и для других орбиталей: s, p, d и f.
Источник статьи: https://habr.com/ru/company/skillfactory/blog/564822/
