Граф – это математическая структура данных, представляющая собой множество связанных элементов. Поскольку графы, по своей сути, являются очень гибкими и позволяют сохранять информацию в знакомой и удобной для восприятия форме, они всегда активно использовались в компьютерной науке и сфере технологий. С появлением же машинного и глубокого обучения, графы обрели ещё бо́льшую популярность, создав новое направление — машинное обучение на графах.
В этой статье я расскажу вам о наиболее полезных библиотеках Python, которые использовал для сетевого/графового анализа, визуализации и машинного обучения. Если говорить конкретнее, то это будут:
Граф – это просто набор взаимосвязанных элементов.

Однако тот факт, что эти элементы (называемые узлами) могут содержать любую информацию и быть связанными любым образом (с помощью рёбер) делает граф наиболее обобщённой структурой данных. На деле любые знакомые нам данные вне зависимости от их сложности можно представить в виде простого графа. Например, изображение – в виде сетки пикселей, а текст – в виде последовательности или цепочки слов.
Вы можете задуматься, а действительно ли графы настолько важны? Дело в том, что некоторые задачи без них попросту нельзя решить или даже сформулировать, поскольку некоторую информацию структурировать невозможно. Представьте такую ситуацию: вам нужно посетить ряд городов, скажем, с туристическими или рабочими целями. У вас есть информация о расстоянии между городами или, например, о стоимости проезда на разных видах транспорта – так даже интереснее. Как в этой ситуации спланировать оптимальный маршрут, чтобы потратить минимальную сумму денег или проехать минимальное расстояние?
Причём это довольно практическая задача – представьте, насколько она актуальна хотя бы в той же логистике – и является примером такой, что без графов решить нельзя. Подумайте о том, как можно представить эти данные, и в любом случае вы, так или иначе, придёте к взвешенному графу (графы, чьи рёбра имеют обозначенную ценность, называются взвешенными). Кстати, если каждый город нужно посетить лишь раз, то у нас уже получится известная задача о коммивояжёре (TSP), решить которую не так-то просто. Одна из причин сложности в том, что число возможных маршрутов растёт очень быстро, и даже для 7 городов их существует аж 360!
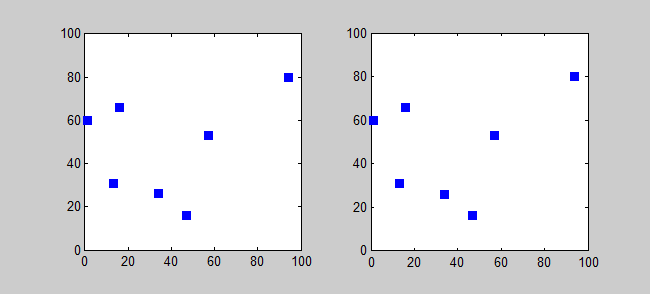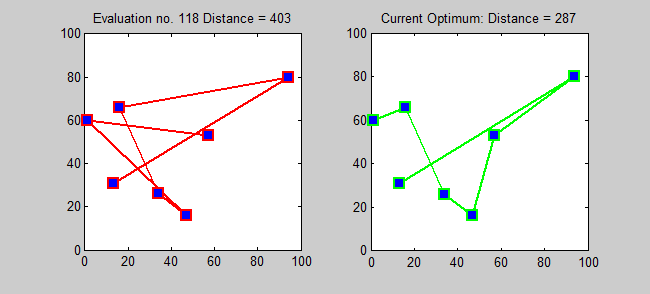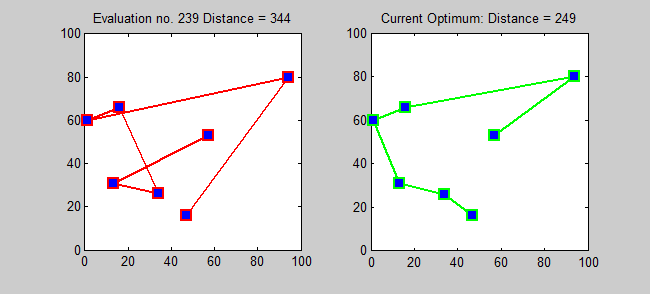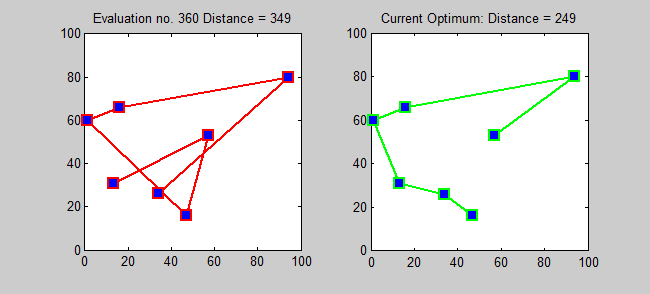
Решение задачи коммивояжёра с 7 городами методом брутфорса
Теория графов была придумана в XVIII веке и использовалась при изучении графов, а также решении различных связанных с ними задач: поиске возможного или оптимального пути в графе, построении и разработке деревьев (особый вид графов) и так далее. Эта теория успешно применялась в социальных науках, химии, биологии и прочих областях знаний. Однако с появлением компьютеров техника использования графов вышла на новый уровень.
Главное здесь то, что сама основа графа – набор связанных элементов, зачастую разных и имеющих разные связи – оказывается очень полезной для моделирования реальных задач и датасетов. Именно здесь к делу подключается машинное обучение на графах, хотя многие поразительные задачи решались и до его появления. Когда человечество собрало всевозможные наборы данных и создало технологии для их моделирования (например, графовые свёрточные сети (GCN), аналогичные свёрточным нейронным сетям (CNN)), перед ним открылась возможность решения широкого спектра задач:
Ниже мы разберём примеры графов из реальной жизни. Одним из самых известных графовых наборов данных является датасет клуба каратэ. В нём каждый узел представляет человека (члена клуба), а каждое ребро – двух членов, которые взаимодействовали вне клуба.

Визуализация датасета клуба каратэ
Типичной задачей здесь является поиск двух групп людей, на которые клуб разделяется после спора двух инструкторов (теперь её можно рассматривать как двоичную (или 2-классовую) классификацию узлов). Этот датасет был собран в 1977 году и стал классическим примером социальной сети людей или структуры сообщества.
Ещё одним видом графов, который хорошо понятен человеку и, следовательно, очень полезен для моделей машинного обучения, является граф знаний. В нём узел представляет некую сущность, или понятие, а ребро указывает на взаимосвязь пары подобных сущностей. Таким образом, структура узел-ребро-узел хранит конкретный факт знаний о мире или некой системе.
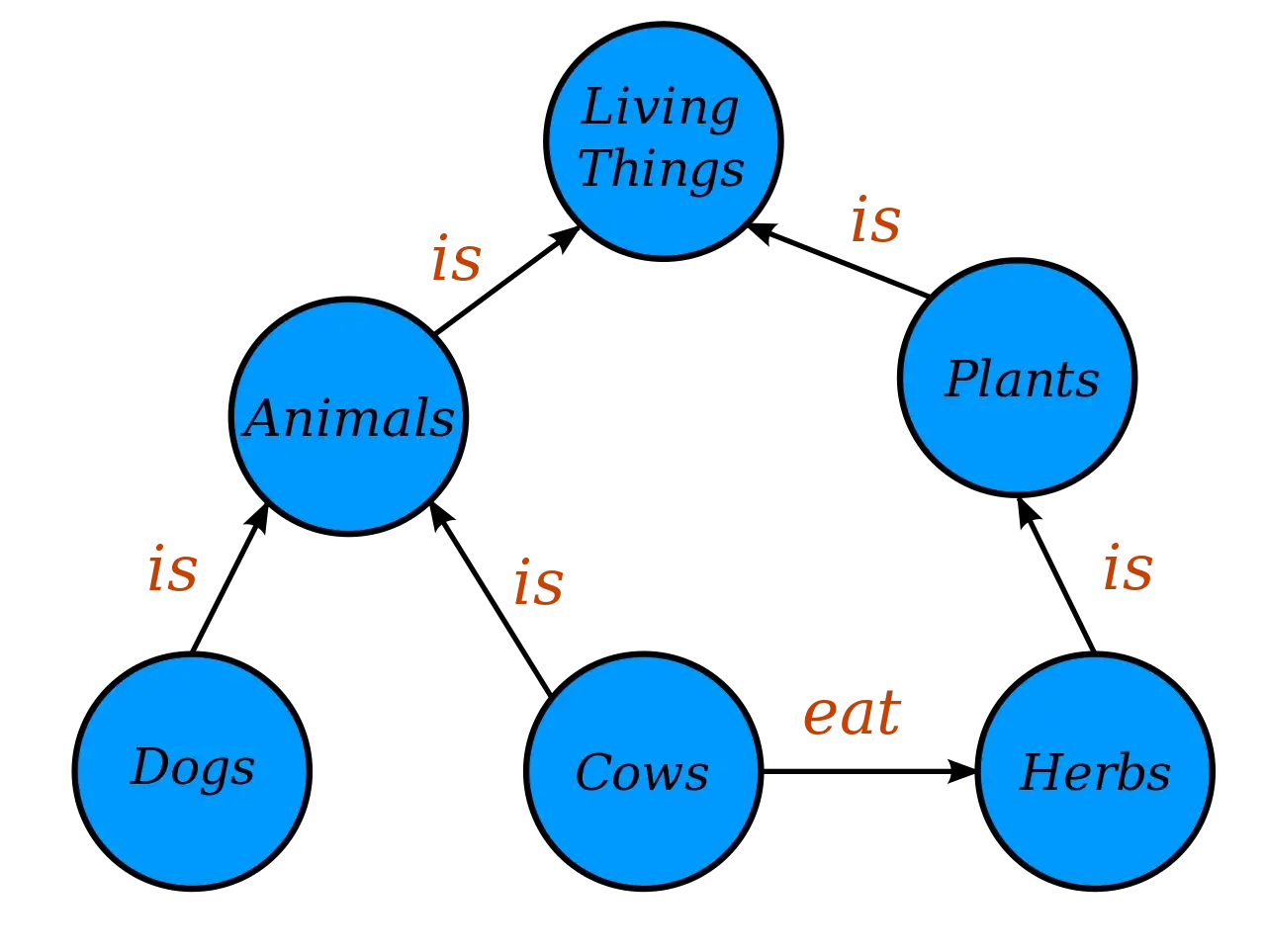
Простой пример графа знаний
В примере выше содержится два вида рёбер: «является» (is) и «ест» (eat), в связи с чем он является мультиграфом. Структура Dogs-is-Animals даёт нам понять, что множество dogs является подмножеством animals. Проще говоря, собаки являются животными.
Wikidata представляет бесплатную базу знаний от Википедии, которая постоянно обновляется и содержит уже более 100 миллионов узлов. В ней присутствует более 400 видов рёбер, среди которых part of, different from, opposite of, population и location, то есть она явно глубоко продумана.
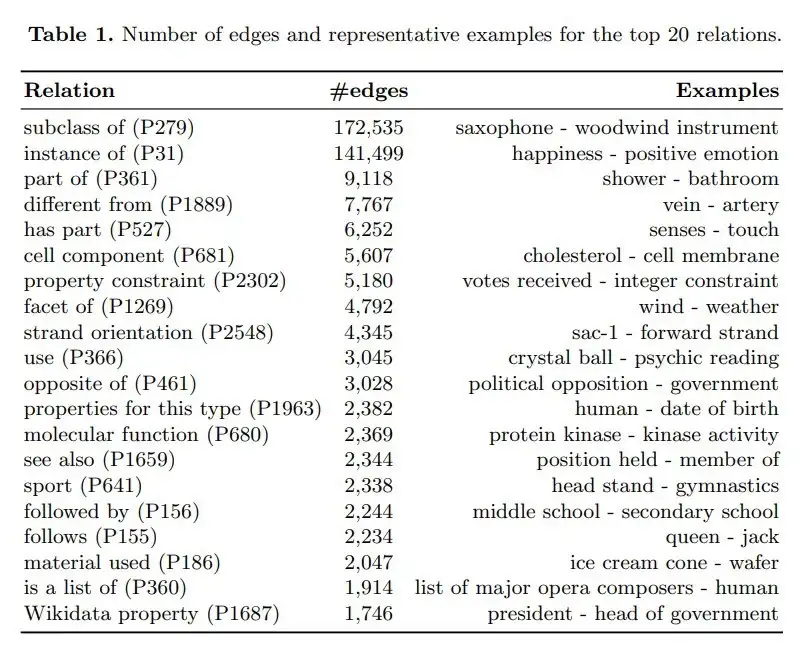
Топ-20 наиболее распространённых связей в базе знаний wikidata на 2020 год
Эта огромная база содержит много информации об окружающем нас мире. Меня до сих пор поражает то, что человечеству удалось собрать все эти данные, и что теперь их могут обрабатывать машины.
Ещё один важный момент – это превосходные возможности wikidata по визуализации. К примеру, здесь вы видите график связанности штатов США. Заметьте, что его никто не рисовал – это просто подграф общего графа wikidata. Мы взяли только американские штаты в качестве узлов и P47 (граничит с) в качестве рёбер.

Связанность штатов США
Взгляните на Wikidata Graph Builder и другие визуализации. Вот некоторые из них, которые лично я нахожу интересными:
Если после краткого обзора у вас возник интерес к более глубокому изучению графов, рекомендую прекрасную работу Gentle Introduction to Graph Neural Networks от Google Research. В этой статье вы сможете найти дополнительные примеры и интерактивные визуализации.
Ещё советую курс Graph Theory Algorithms course на freeCodeCamp.org, рассказывающий о различных алгоритмах теории графов, или Stanford CS224W: Machine Learning with Graphs, который поможет встать на путь освоения машинного обучения на графах.
Ну а мы далее перейдём к знакомству с библиотеками Python.
Если вам потребуется проделать какие-либо операции над графами с помощью Python, то вы довольно быстро наткнётесь на библиотеку NetworkX. Это, пожалуй, наиболее фундаментальная и распространённая библиотека для сетевого анализа, предоставляющая широкую функциональность:
Эта библиотека довольно интуитивна и удобна в использовании. При этом большая часть основ вроде графовых структур данных будут прежними или по меньшей мере похожими во всех популярных библиотеках для работы с графами. Для лучшего понимания можете создать простой граф и визуализировать его с помощью следующего кода:
import matplotlib.pyplot as plt
import networkx as nx
G = nx.Graph() # создаём объект графа
# определяем список узлов (ID узлов)
nodes = [1, 2, 3, 4, 5]
# определяем список рёбер
# список кортежей, каждый из которых представляет ребро
# кортеж (id_1, id_2) означает, что узлы id_1 и id_2 соединены ребром
edges = [(1, 2), (1, 3), (2, 3), (2, 4), (3, 5), (5, 5)]
# добавляем информацию в объект графа
G.add_nodes_from(nodes)
G.add_edges_from(edges)
# рисуем граф и отображаем его
nx.draw(G, with_labels=True, font_weight='bold')
plt.show()
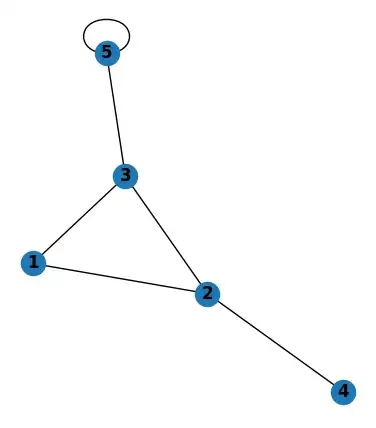
Простая визуализация NetworkX
Если говорить об алгоритмах, то NetworkX в этом плане весьма впечатляет, предлагая сотни их готовых вариантов.
В общем и целом – это эффективная, масштабируемая и мощная библиотека, которая определённо пригодится при анализе графов.
https://networkx.org/
Если рассматривать использование NetworkX для визуализации, то она вполне подойдёт для небольших графов. В случаях же, когда вам требуется бо́льшая гибкость или интерактивность, предпочтительнее обратить внимание на PyVis. Ситуация здесь аналогична выбору между matplotlib и plotly. Matplotlib отлично подходит для построения быстрых и простых визуализаций, но если вы хотите иметь возможность взаимодействовать с графом или поделиться им с кем-то ещё, то лучше будет задействовать более мощные инструменты.
Будучи построенной на базе библиотеки VisJS, PyVis позволяет создавать в браузере интерактивные визуализации с помощью простого кода. Давайте используем её для построения графа из примера выше.
from pyvis.network import Network
net = Network() # создаём объект графа
# добавление узлов
net.add_nodes(
[1, 2, 3, 4, 5], # node ids
label=['Node #1', 'Node #2', 'Node #3', 'Node #4', 'Node #5'], # node labels
# node titles (display on mouse hover)
title=['Main node', 'Just node', 'Just node', 'Just node', 'Node with self-loop'],
color=['#d47415', '#22b512', '#42adf5', '#4a21b0', '#e627a3'] # node colors (HEX)
)
# добавляем тот же список узлов, что и в предыдущем примере
net.add_edges([(1, 2), (1, 3), (2, 3), (2, 4), (3, 5), (5, 5)])
net.show('graph.html') # save visualization in 'graph.html'
Этот код создаст файл graph.html, открыв который, вы сможете взаимодействовать с вашей визуализацией: приближать, перетаскивать её элементы и выполнять прочие манипуляции.
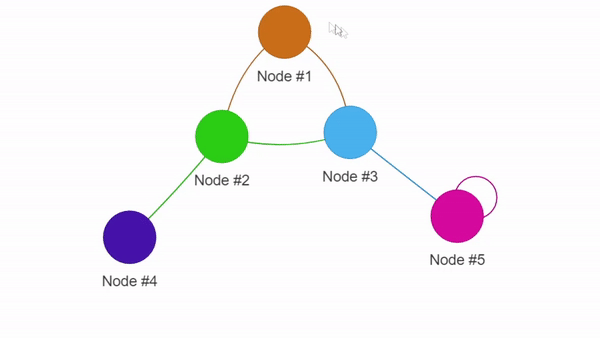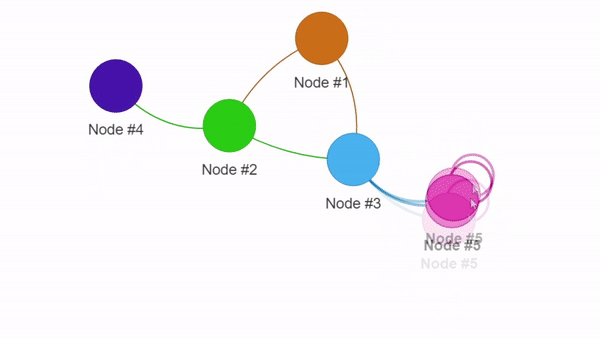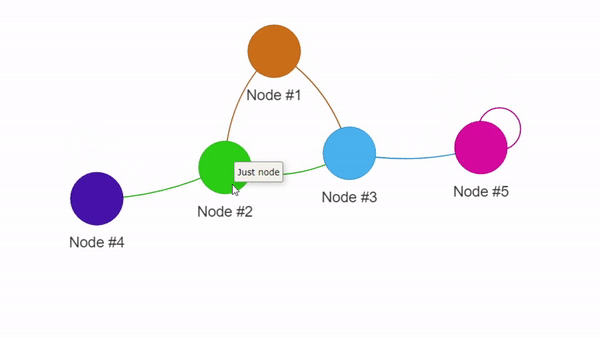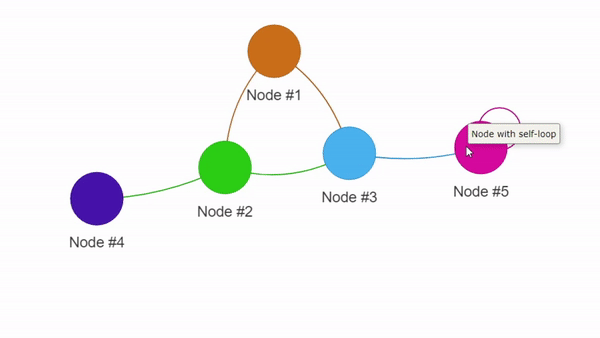
Пример визуализации с помощью PyVis
Интересно выглядит, не так ли? Эта библиотека даже позволяет использовать веб-UI для динамической подстройки конфигурации дисплея. Ознакомиться со всеми её основными возможностями можно в официальной документации.
https://pyvis.readthedocs.io/en/latest/
Теперь перейдём к более продвинутой теме – машинному обучению на графах. Здесь я представлю вам две наиболее популярные библиотеки: DGL и PyG.
DGL (Deep Graph Library) появилась в 2018 году. В противоположность PyG (PyTorch Geometric), построенной на базе PyTorch и работающей только с тензорами PyTorch, DGL поддерживает множество фреймворков машинного обучения, включая PyTorch, TensorFlow и MXNet.
Обе библиотеки предлагают известные реализации графовых нейронных сетей (GNN), такие как GraphSAGE, GAT (Graph Attention Network), GIN (Graph Isomorphism Network) и прочие. С их помощью будет несложно построить модель из готовых блоков – этот процесс очень напоминает простой PyTorch или TensorFlow.
Вот как в PyG создаётся двухслойная GCN-модель для классификации узлов:
import torch
from torch_geometric.nn import GCNConv
class PyG_GCN(torch.nn.Module):
def __init__(self, in_channels, hidden_channels, out_channels):
super().__init__()
# определяем два слоя графовой свёрточной сети
self.conv1 = GCNConv(in_channels, hidden_channels)
self.conv2 = GCNConv(hidden_channels, out_channels)
def forward(self, x, edge_index):
# x: матрица признаков узлов в форме (num_nodes, in_channels)
# edge_index: матрица связей графа в форме (2, num_edges)
x = self.conv1(x, edge_index).relu()
x = self.conv2(x, edge_index)
return x
# для базы данных цитирования Cora
num_features = 1433
num_classes = 7
num_hidden = 16
model = PyG_GCN(num_features, num_hidden, num_classes)
А вот тот же код для DGL:
import torch
import torch.nn.functional as F
from dgl.nn import GraphConv
class DGL_GCN(torch.nn.Module):
def __init__(self, in_channels, hidden_channels, out_channels):
super(DGL_GCN, self).__init__()
# определяем два слоя графовой свёрточной сети
self.conv1 = GraphConv(in_channels, hidden_channels)
self.conv2 = GraphConv(hidden_channels, out_channels)
def forward(self, g, in_feat):
# g: объект графа в DGL, содержащий информацию о связях узлов
# in_feat: матрица признаков узлов в формате (num_nodes, in_channels)
h = self.conv1(g, in_feat)
h = F.relu(h)
h = self.conv2(g, h)
return h
# для базы данных цитирования Cora
num_features = 1433
num_classes = 7
num_hidden = 16
model = DGL_GCN(num_features, num_hidden, num_classes)
Если вы знакомы с глубоким обучением и PyTorch, то оба этих фрагмента будут достаточно вам ясны.
Как видите, определения модели в обеих библиотеках очень похожи. При этом обучающий цикл в случае PyG можно написать с помощью базового PyTorch, а вот в случае DGL он потребует внесения некоторых изменений (поскольку графовые объекты в DGL хранят весь набор данных, и к обучающей/валидационной/тестовой выборкам необходимо обращаться с помощью двоичных масок).
Здесь у нас есть некоторое отличие в представлении данных: мы видим, что обусловлено оно по меньшей мере различными входными параметрами для метода forward. По факту PyG сохраняет всё в виде тензоров PyTorch, а в DGL для этого необходимо использовать отдельный объект графа, и внутреннее устройство этой библиотеки больше напоминает NetworkX.
Однако особой проблемы тут нет – вы можете преобразовывать объект графа PyG в граф DGL и наоборот с помощью всего нескольких строк кода. Более же существенными здесь будут вопросы: «Чем ещё отличаются эти библиотеки, и какую следует выбирать?»
Пытаясь понять, какая из них лучше, вы будете постоянно приходить к одному и тому же ответу: «Попробуй обе и выбирай более подходящую». Хорошо, но чем они вообще отличаются? Здесь тоже нет чёткой ясности, и типичный ответ будет указывать на их значительное сходство.
Так оно и есть. Более того, вы сами видели это на примере кода выше. Естественно, при углублённом анализе кое-какие отличия найти можно: вот хороший список ресурсов, включая размышления от самих авторов библиотек, а здесь вы найдёте их подробное разностороннее сравнение.
Как правило, для выбора наиболее подходящей действительно нужно будет попробовать обе. Если говорить о выраженных отличиях, то DGL имеет более низкоуровневый API, что делает её менее удобной и понятной при реализации новых идей. Зато эта библиотека является более гибкой – она не ограничена сетями передачи сообщений (классические графовые свёрточные сети) и реализует ряд принципов, которые PyG предоставить не может, к примеру, Tree-LSTM.
PyTorch Geometric, напротив, обладает максимально простым в использовании API, в связи с чем больше привлекает исследователей, которых интересует быстрое воплощение свежих идей, например, новых реализаций GNN. В последнее время популярность PyG растёт, чему способствовало внедрение важных обновлений в версии 2.0 и высокая активность сильных участников проекта, среди которых присутствует Стэнфордский университет.

Число поисковых запросов DGL и PyG за последние 5 лет
Так что я рекомендую вам попробовать обе этих библиотеки, начиная с PyG.
Если вы работаете над относительно знакомой задачей с графами (будто то классификация узлов, классификация графов и так далее), то и PyG, и DGL предлагают для этого множество реализаций GNN. При этом с помощью PyG будет проще реализовать собственную GNN в качестве любого исследовательского проекта.
Однако, если вы хотите получить полный контроль над внутренними процессами или реализовать что-то более сложное, нежели структуру передачи сообщений, ваш выбор скорее падёт на DGL.
Целевая аудитория этой статьи, то есть люди, интересующиеся работой с графами, довольно мала. Что ж, машинное обучение является относительно молодой наукой, а машинное обучение на графах тем более. Последнее привлекает внимание в основном исследовательского сообщества, хотя по факту используется в таких важных направлениях, как рекомендательные системы и биологические/химические исследования.
Как бы то ни было, надеюсь, что эти материалы оказались для вас интересными и полезными.
 habr.com
habr.com
В этой статье я расскажу вам о наиболее полезных библиотеках Python, которые использовал для сетевого/графового анализа, визуализации и машинного обучения. Если говорить конкретнее, то это будут:
- NetworkX для общего анализа графов;
- PyVis для интерактивной визуализации графов прямо в браузере;
- PyG и DGL для решения различных задач в области машинного обучения на графах.
Краткое знакомство с теорией графов и машинным обучением на графах
Граф – это просто набор взаимосвязанных элементов.

Однако тот факт, что эти элементы (называемые узлами) могут содержать любую информацию и быть связанными любым образом (с помощью рёбер) делает граф наиболее обобщённой структурой данных. На деле любые знакомые нам данные вне зависимости от их сложности можно представить в виде простого графа. Например, изображение – в виде сетки пикселей, а текст – в виде последовательности или цепочки слов.
Вы можете задуматься, а действительно ли графы настолько важны? Дело в том, что некоторые задачи без них попросту нельзя решить или даже сформулировать, поскольку некоторую информацию структурировать невозможно. Представьте такую ситуацию: вам нужно посетить ряд городов, скажем, с туристическими или рабочими целями. У вас есть информация о расстоянии между городами или, например, о стоимости проезда на разных видах транспорта – так даже интереснее. Как в этой ситуации спланировать оптимальный маршрут, чтобы потратить минимальную сумму денег или проехать минимальное расстояние?
Причём это довольно практическая задача – представьте, насколько она актуальна хотя бы в той же логистике – и является примером такой, что без графов решить нельзя. Подумайте о том, как можно представить эти данные, и в любом случае вы, так или иначе, придёте к взвешенному графу (графы, чьи рёбра имеют обозначенную ценность, называются взвешенными). Кстати, если каждый город нужно посетить лишь раз, то у нас уже получится известная задача о коммивояжёре (TSP), решить которую не так-то просто. Одна из причин сложности в том, что число возможных маршрутов растёт очень быстро, и даже для 7 городов их существует аж 360!

Решение задачи коммивояжёра с 7 городами методом брутфорса
Теория графов была придумана в XVIII веке и использовалась при изучении графов, а также решении различных связанных с ними задач: поиске возможного или оптимального пути в графе, построении и разработке деревьев (особый вид графов) и так далее. Эта теория успешно применялась в социальных науках, химии, биологии и прочих областях знаний. Однако с появлением компьютеров техника использования графов вышла на новый уровень.
Главное здесь то, что сама основа графа – набор связанных элементов, зачастую разных и имеющих разные связи – оказывается очень полезной для моделирования реальных задач и датасетов. Именно здесь к делу подключается машинное обучение на графах, хотя многие поразительные задачи решались и до его появления. Когда человечество собрало всевозможные наборы данных и создало технологии для их моделирования (например, графовые свёрточные сети (GCN), аналогичные свёрточным нейронным сетям (CNN)), перед ним открылась возможность решения широкого спектра задач:
- на уровне узлов (например, классификация узлов) – присваивание метки каждому узлу в графе. Чуть ниже будет приведён её пример, в котором нужно поделить группу людей на два кластера, исходя из информации об их связях друг с другом. Но при этом вариантов её применения очень много. Основная идея здесь происходит из области общественных наук, которая гласит, что мы зависим от нашего окружения. В действительности любую сущность можно более эффективно классифицировать, если учесть не только некоторые её характеристики, но и данные о соседях. К примеру, если ваши друзья курят, то и вы наверняка тоже. Ну или, если ваши друзья ходят в спортзал, то это, скорее всего, относится и к вам.
- на уровне рёбер (например, прогнозирование рёбер) – подразумевают прогнозирование наличия ребра между двух узлов или, чаще всего, типа ребра (графы, имеющие несколько типов рёбер, называются мультиграфами). Такой вид задач очень актуален для работы с графами знаний, о которых мы вскоре узнаем подробнее.
- на уровне графов. Сюда относятся классификация графов, генерация графов и так далее. Это направление особенно полезно для биологии и химии, поскольку молекулы можно представить как графы. Формулировка классификация молекул (выяснение, обладает ли молекула определёнными свойствами) или генерация молекул (особенно медицинских препаратов) звучит куда круче, чем «задачи уровня графов».
Ниже мы разберём примеры графов из реальной жизни. Одним из самых известных графовых наборов данных является датасет клуба каратэ. В нём каждый узел представляет человека (члена клуба), а каждое ребро – двух членов, которые взаимодействовали вне клуба.

Визуализация датасета клуба каратэ
Типичной задачей здесь является поиск двух групп людей, на которые клуб разделяется после спора двух инструкторов (теперь её можно рассматривать как двоичную (или 2-классовую) классификацию узлов). Этот датасет был собран в 1977 году и стал классическим примером социальной сети людей или структуры сообщества.
Ещё одним видом графов, который хорошо понятен человеку и, следовательно, очень полезен для моделей машинного обучения, является граф знаний. В нём узел представляет некую сущность, или понятие, а ребро указывает на взаимосвязь пары подобных сущностей. Таким образом, структура узел-ребро-узел хранит конкретный факт знаний о мире или некой системе.

Простой пример графа знаний
В примере выше содержится два вида рёбер: «является» (is) и «ест» (eat), в связи с чем он является мультиграфом. Структура Dogs-is-Animals даёт нам понять, что множество dogs является подмножеством animals. Проще говоря, собаки являются животными.
Wikidata представляет бесплатную базу знаний от Википедии, которая постоянно обновляется и содержит уже более 100 миллионов узлов. В ней присутствует более 400 видов рёбер, среди которых part of, different from, opposite of, population и location, то есть она явно глубоко продумана.

Топ-20 наиболее распространённых связей в базе знаний wikidata на 2020 год
Эта огромная база содержит много информации об окружающем нас мире. Меня до сих пор поражает то, что человечеству удалось собрать все эти данные, и что теперь их могут обрабатывать машины.
Ещё один важный момент – это превосходные возможности wikidata по визуализации. К примеру, здесь вы видите график связанности штатов США. Заметьте, что его никто не рисовал – это просто подграф общего графа wikidata. Мы взяли только американские штаты в качестве узлов и P47 (граничит с) в качестве рёбер.

Связанность штатов США
Взгляните на Wikidata Graph Builder и другие визуализации. Вот некоторые из них, которые лично я нахожу интересными:
- карта связей между мастером и учеником, начиная со времён Сократа и заканчивая периодом эллинизма;
- интерактивные временные линии с историческими событиями;
- семейное древо панды Pan Pan.
▍ Подробнее о графах
Если после краткого обзора у вас возник интерес к более глубокому изучению графов, рекомендую прекрасную работу Gentle Introduction to Graph Neural Networks от Google Research. В этой статье вы сможете найти дополнительные примеры и интерактивные визуализации.
Ещё советую курс Graph Theory Algorithms course на freeCodeCamp.org, рассказывающий о различных алгоритмах теории графов, или Stanford CS224W: Machine Learning with Graphs, который поможет встать на путь освоения машинного обучения на графах.
Ну а мы далее перейдём к знакомству с библиотеками Python.
NetworkX — общий анализ графов
Если вам потребуется проделать какие-либо операции над графами с помощью Python, то вы довольно быстро наткнётесь на библиотеку NetworkX. Это, пожалуй, наиболее фундаментальная и распространённая библиотека для сетевого анализа, предоставляющая широкую функциональность:
- структуры данных для хранения и обработки ненаправленных/направленных графов и мультиграфов;
- множество готовых графовых алгоритмов;
- базовые инструменты визуализации.
Эта библиотека довольно интуитивна и удобна в использовании. При этом большая часть основ вроде графовых структур данных будут прежними или по меньшей мере похожими во всех популярных библиотеках для работы с графами. Для лучшего понимания можете создать простой граф и визуализировать его с помощью следующего кода:
import matplotlib.pyplot as plt
import networkx as nx
G = nx.Graph() # создаём объект графа
# определяем список узлов (ID узлов)
nodes = [1, 2, 3, 4, 5]
# определяем список рёбер
# список кортежей, каждый из которых представляет ребро
# кортеж (id_1, id_2) означает, что узлы id_1 и id_2 соединены ребром
edges = [(1, 2), (1, 3), (2, 3), (2, 4), (3, 5), (5, 5)]
# добавляем информацию в объект графа
G.add_nodes_from(nodes)
G.add_edges_from(edges)
# рисуем граф и отображаем его
nx.draw(G, with_labels=True, font_weight='bold')
plt.show()

Простая визуализация NetworkX
Если говорить об алгоритмах, то NetworkX в этом плане весьма впечатляет, предлагая сотни их готовых вариантов.
В общем и целом – это эффективная, масштабируемая и мощная библиотека, которая определённо пригодится при анализе графов.
▍ Ссылка
https://networkx.org/
PyVis — интерактивная визуализация графов
Если рассматривать использование NetworkX для визуализации, то она вполне подойдёт для небольших графов. В случаях же, когда вам требуется бо́льшая гибкость или интерактивность, предпочтительнее обратить внимание на PyVis. Ситуация здесь аналогична выбору между matplotlib и plotly. Matplotlib отлично подходит для построения быстрых и простых визуализаций, но если вы хотите иметь возможность взаимодействовать с графом или поделиться им с кем-то ещё, то лучше будет задействовать более мощные инструменты.
Будучи построенной на базе библиотеки VisJS, PyVis позволяет создавать в браузере интерактивные визуализации с помощью простого кода. Давайте используем её для построения графа из примера выше.
from pyvis.network import Network
net = Network() # создаём объект графа
# добавление узлов
net.add_nodes(
[1, 2, 3, 4, 5], # node ids
label=['Node #1', 'Node #2', 'Node #3', 'Node #4', 'Node #5'], # node labels
# node titles (display on mouse hover)
title=['Main node', 'Just node', 'Just node', 'Just node', 'Node with self-loop'],
color=['#d47415', '#22b512', '#42adf5', '#4a21b0', '#e627a3'] # node colors (HEX)
)
# добавляем тот же список узлов, что и в предыдущем примере
net.add_edges([(1, 2), (1, 3), (2, 3), (2, 4), (3, 5), (5, 5)])
net.show('graph.html') # save visualization in 'graph.html'
Этот код создаст файл graph.html, открыв который, вы сможете взаимодействовать с вашей визуализацией: приближать, перетаскивать её элементы и выполнять прочие манипуляции.

Пример визуализации с помощью PyVis
Интересно выглядит, не так ли? Эта библиотека даже позволяет использовать веб-UI для динамической подстройки конфигурации дисплея. Ознакомиться со всеми её основными возможностями можно в официальной документации.
▍ Ссылка
https://pyvis.readthedocs.io/en/latest/
Машинное обучение на графах с помощью DGL и PyG
Теперь перейдём к более продвинутой теме – машинному обучению на графах. Здесь я представлю вам две наиболее популярные библиотеки: DGL и PyG.
DGL (Deep Graph Library) появилась в 2018 году. В противоположность PyG (PyTorch Geometric), построенной на базе PyTorch и работающей только с тензорами PyTorch, DGL поддерживает множество фреймворков машинного обучения, включая PyTorch, TensorFlow и MXNet.
Обе библиотеки предлагают известные реализации графовых нейронных сетей (GNN), такие как GraphSAGE, GAT (Graph Attention Network), GIN (Graph Isomorphism Network) и прочие. С их помощью будет несложно построить модель из готовых блоков – этот процесс очень напоминает простой PyTorch или TensorFlow.
Вот как в PyG создаётся двухслойная GCN-модель для классификации узлов:
import torch
from torch_geometric.nn import GCNConv
class PyG_GCN(torch.nn.Module):
def __init__(self, in_channels, hidden_channels, out_channels):
super().__init__()
# определяем два слоя графовой свёрточной сети
self.conv1 = GCNConv(in_channels, hidden_channels)
self.conv2 = GCNConv(hidden_channels, out_channels)
def forward(self, x, edge_index):
# x: матрица признаков узлов в форме (num_nodes, in_channels)
# edge_index: матрица связей графа в форме (2, num_edges)
x = self.conv1(x, edge_index).relu()
x = self.conv2(x, edge_index)
return x
# для базы данных цитирования Cora
num_features = 1433
num_classes = 7
num_hidden = 16
model = PyG_GCN(num_features, num_hidden, num_classes)
А вот тот же код для DGL:
import torch
import torch.nn.functional as F
from dgl.nn import GraphConv
class DGL_GCN(torch.nn.Module):
def __init__(self, in_channels, hidden_channels, out_channels):
super(DGL_GCN, self).__init__()
# определяем два слоя графовой свёрточной сети
self.conv1 = GraphConv(in_channels, hidden_channels)
self.conv2 = GraphConv(hidden_channels, out_channels)
def forward(self, g, in_feat):
# g: объект графа в DGL, содержащий информацию о связях узлов
# in_feat: матрица признаков узлов в формате (num_nodes, in_channels)
h = self.conv1(g, in_feat)
h = F.relu(h)
h = self.conv2(g, h)
return h
# для базы данных цитирования Cora
num_features = 1433
num_classes = 7
num_hidden = 16
model = DGL_GCN(num_features, num_hidden, num_classes)
Если вы знакомы с глубоким обучением и PyTorch, то оба этих фрагмента будут достаточно вам ясны.
Как видите, определения модели в обеих библиотеках очень похожи. При этом обучающий цикл в случае PyG можно написать с помощью базового PyTorch, а вот в случае DGL он потребует внесения некоторых изменений (поскольку графовые объекты в DGL хранят весь набор данных, и к обучающей/валидационной/тестовой выборкам необходимо обращаться с помощью двоичных масок).
Здесь у нас есть некоторое отличие в представлении данных: мы видим, что обусловлено оно по меньшей мере различными входными параметрами для метода forward. По факту PyG сохраняет всё в виде тензоров PyTorch, а в DGL для этого необходимо использовать отдельный объект графа, и внутреннее устройство этой библиотеки больше напоминает NetworkX.
Однако особой проблемы тут нет – вы можете преобразовывать объект графа PyG в граф DGL и наоборот с помощью всего нескольких строк кода. Более же существенными здесь будут вопросы: «Чем ещё отличаются эти библиотеки, и какую следует выбирать?»
DGL или PyG
Пытаясь понять, какая из них лучше, вы будете постоянно приходить к одному и тому же ответу: «Попробуй обе и выбирай более подходящую». Хорошо, но чем они вообще отличаются? Здесь тоже нет чёткой ясности, и типичный ответ будет указывать на их значительное сходство.
Так оно и есть. Более того, вы сами видели это на примере кода выше. Естественно, при углублённом анализе кое-какие отличия найти можно: вот хороший список ресурсов, включая размышления от самих авторов библиотек, а здесь вы найдёте их подробное разностороннее сравнение.
Как правило, для выбора наиболее подходящей действительно нужно будет попробовать обе. Если говорить о выраженных отличиях, то DGL имеет более низкоуровневый API, что делает её менее удобной и понятной при реализации новых идей. Зато эта библиотека является более гибкой – она не ограничена сетями передачи сообщений (классические графовые свёрточные сети) и реализует ряд принципов, которые PyG предоставить не может, к примеру, Tree-LSTM.
PyTorch Geometric, напротив, обладает максимально простым в использовании API, в связи с чем больше привлекает исследователей, которых интересует быстрое воплощение свежих идей, например, новых реализаций GNN. В последнее время популярность PyG растёт, чему способствовало внедрение важных обновлений в версии 2.0 и высокая активность сильных участников проекта, среди которых присутствует Стэнфордский университет.

Число поисковых запросов DGL и PyG за последние 5 лет
Так что я рекомендую вам попробовать обе этих библиотеки, начиная с PyG.
Если вы работаете над относительно знакомой задачей с графами (будто то классификация узлов, классификация графов и так далее), то и PyG, и DGL предлагают для этого множество реализаций GNN. При этом с помощью PyG будет проще реализовать собственную GNN в качестве любого исследовательского проекта.
Однако, если вы хотите получить полный контроль над внутренними процессами или реализовать что-то более сложное, нежели структуру передачи сообщений, ваш выбор скорее падёт на DGL.
▍ Ссылки
Заключение
Целевая аудитория этой статьи, то есть люди, интересующиеся работой с графами, довольно мала. Что ж, машинное обучение является относительно молодой наукой, а машинное обучение на графах тем более. Последнее привлекает внимание в основном исследовательского сообщества, хотя по факту используется в таких важных направлениях, как рекомендательные системы и биологические/химические исследования.
Как бы то ни было, надеюсь, что эти материалы оказались для вас интересными и полезными.

Графы в Python: введение и знакомство с лучшими библиотеками
Граф – это математическая структура данных, представляющая собой множество связанных элементов. Поскольку графы, по своей сути, являются очень гибкими и позволяют сохранять информацию в знакомой и...
