Используя новый алгоритм упаковки, в Graphcore ускорили обработку естественного языка более чем в 2 раза при обучении BERT-Large. Метод упаковки удаляет заполнение, что позволяет значительно повысить эффективность вычислений. В Graphcore предполагают, что это также может применяться в геномике, в моделях фолдинга белков и других моделях с перекошенным распределением длины, оказывая гораздо более широкое влияние на различные отрасли и приложения. В новой работе Graphcore представили высокоэффективный алгоритм гистограммной упаковки с неотрицательными наименьшими квадратами (или NNLSHP), а также алгоритм BERT, применяемый к упакованным последовательностям. К старту курса о машинном и глубоком обучении представляем перевод обзора соответствующей публикации на ArXiv от её авторов. Ссылку на репозиторий вы найдёте в конце статьи.
Мы очень удивились, узнав, что в нашем собственном обучающем приложении BERT-Large, использующем набор данных Wikipedia, 50 % токенов набора данных были заполнениями, что привело к большому количеству напрасных вычислений.
Заполнение последовательностей для выравнивания их длины — распространённый подход, используемый в графических процессорах, но мы решили, что стоит попробовать другой. Последовательности имеют большой разброс длины по двум причинам:
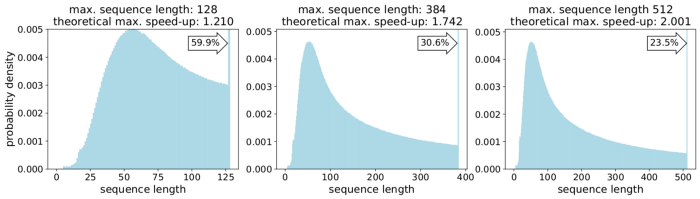 Рисунок 1 — Распределение данных в Википедии. Изображение автора
Рисунок 1 — Распределение данных в Википедии. Изображение автора
Относится ли это только к Википедии? Нет. А специфично ли явление для языка? Снова нет. На самом деле перекосы в распределении длины встречаются повсеместно: в языке, геномике и в фолдинге белков. На рисунках 2 и 3 показаны распределения в наборах данных SQuAD 1.1 и GLUE.
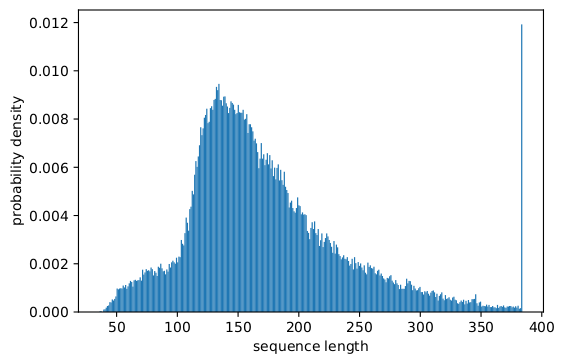 Рисунок 2 — Гистограмма длины последовательностей набора данных SQuAD 1.1 BERT для максимальной длины последовательности 384. Изображение автора
Рисунок 2 — Гистограмма длины последовательностей набора данных SQuAD 1.1 BERT для максимальной длины последовательности 384. Изображение автора
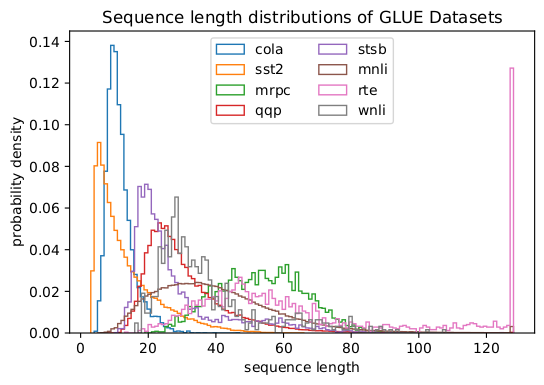 Рисунок 3 — Гистограммы длины последовательности в наборе данных GLUE для максимальной длины последовательности 128. Изображение автора
Рисунок 3 — Гистограммы длины последовательности в наборе данных GLUE для максимальной длины последовательности 128. Изображение автора
Как возможно работать с различными длинами, избегая при этом вычислительных потерь? Существующие подходы требуют различных вычислительных ядер для разных длин или для инженера, который должен программно удалять заполнение, а затем множество раз добавлять её обратно для каждого блока внимания и расчёта потерь. Экономия вычислений за счёт раздувания кода и его усложнения была непривлекательна, поэтому мы искали что-то лучшее.
Нельзя ли просто собрать несколько последовательностей в пакет с максимальной длиной и обработать их все вместе? Оказывается, можно! Этот подход требует трёх ключевых компонентов:
Так почему бы не попробовать 4 последовательности в последовательности? Это увеличило количество комбинаций с 22 000 до 940 000, что было слишком много для нашего первого подхода к моделированию. Кроме того, глубина 3 уже достигла поразительно высокой эффективности. Сначала мы думали, что использование более трёх последовательностей в пакете увеличит вычислительные затраты и повлияет на сходимость во время обучения. Однако для поддержки таких приложений, как выводы, которые требуют ещё более быстрой упаковки в реальном времени, мы разработали высокоэффективный алгоритм гистограммной упаковки с неотрицательными наименьшими квадратами (NNLSHP).
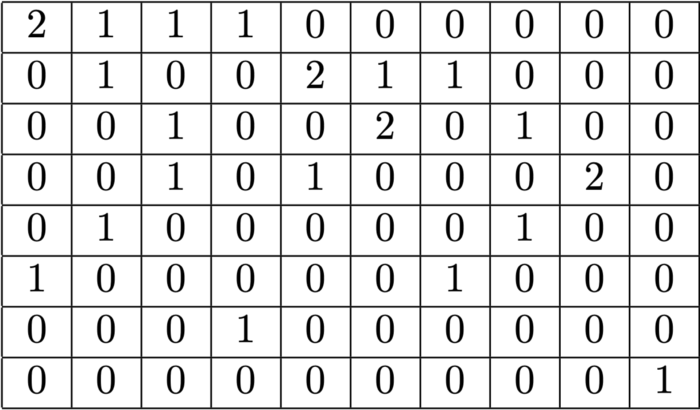 Рисунок 4 — Пример матрицы стратегий для длины последовательности 8 и глубины упаковки 3. Строки обозначают последовательности длины 1–8, которые упаковываются вместе, а столбцы — все возможные комбинации длин в упаковке без определённого порядка.
Рисунок 4 — Пример матрицы стратегий для длины последовательности 8 и глубины упаковки 3. Строки обозначают последовательности длины 1–8, которые упаковываются вместе, а столбцы — все возможные комбинации длин в упаковке без определённого порядка.
В конце нам пришлось исправить некоторые образцы, которым не была назначена стратегия, но их количество было минимальным. Мы также разработали вариационный решатель, который обеспечивает упаковку каждой последовательности, потенциально с заполнением, и имеет вес, зависящий от заполнения. Это заняло гораздо больше времени, а решение оказалось ненамного лучше.

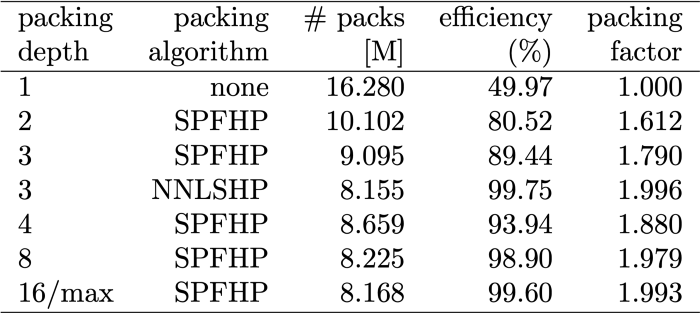 Таблица 1 — Основные результаты работы предложенных алгоритмов упаковки (SPFHP и NNLSHP) на примере Википедии (изображение автора)
Таблица 1 — Основные результаты работы предложенных алгоритмов упаковки (SPFHP и NNLSHP) на примере Википедии (изображение автора)
 Таблица 2 — Результаты работы предложенных алгоритмов упаковки для в предварительно обученной SQUaD 1.1 BERT. Изображение автора
Таблица 2 — Результаты работы предложенных алгоритмов упаковки для в предварительно обученной SQUaD 1.1 BERT. Изображение автора
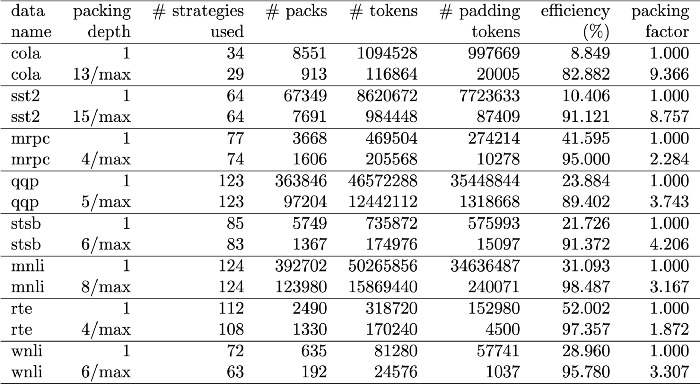 Таблица 3 — Производительность предложенных алгоритмов упаковки для набора данных GLUE. Отображаются только базовые результаты и результаты упаковки SPFHP без ограничения глубины упаковки
Таблица 3 — Производительность предложенных алгоритмов упаковки для набора данных GLUE. Отображаются только базовые результаты и результаты упаковки SPFHP без ограничения глубины упаковки
mask = np.array([[1, 1, 1, 2, 2]]) # input
zero_one_mask = tf.equal(mask, mask.T) # 0, 1 mask
# for use with softmax:
softmax_mask = tf.where(zero_one_mask, 0, -1000)
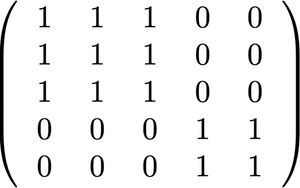 Рисунок 5 — Пример маски ноль–один
Рисунок 5 — Пример маски ноль–один
Для расчёта потерь, принципиально, последовательности распаковываются и рассчитываются потери, в итоге получаем среднее значение потерь по последовательностям (вместо пакетов). Код потерь MLM выглядит следующим образом:
# The number of sequences in each batch may vary
sequences_in_batch = tf.reduce_sum(tf.reduce_max(masked_lm_weight, -1))
sequences_in_batch = tf.cast(sequences_in_batch, tf.float32)
# Create the 0/1 mask that will be used to un-packed sequences
masked_lm_weight = tf.reshape(masked_lm_weight, [B, 1, -1])
sequence_selection = tf.reshape(tf.range(1, max_sequences_per_pack + 1), [1, -1, 1])
sequence_selection = tf.cast(masked_lm_weight == sequence_selection, tf.float32)
# Apply the mask to un-pack the loss per sequence
nll_per_token = tf.reshape(nll_per_token, [B, 1, -1])
nll_per_sequence = sequence_selection * nll_per_token
# Normalize the per-sequence loss by the number of mlm-tokens in the sequence (as is standard)
attempted = tf.reduce_sum(sequence_selection, -1, keepdims=True)
attempted = attempted + tf.cast(attempted == 0, tf.float32) # prevent NaNs when dividing by attempted
nll_per_sequence = nll_per_sequence/attempted
# Average per-batch loss (so contributions from different batches are comparable)
lm_loss = tf.reduce_sum(nll_per_sequence)/sequences_in_batch
Пример кода расчёта потерь
Для потерь NSP и точности принцип тот же. В опубликованных примерах вы найдёте соответствующий код и наш фреймворк PopART.
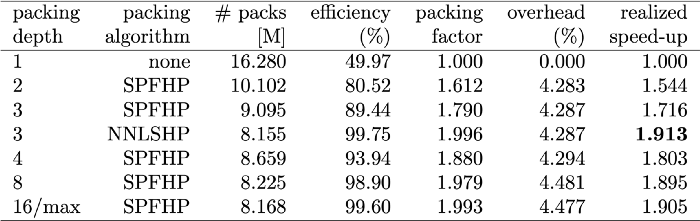 Таблица 4 — Сравнение скорости работы предложенных алгоритмов упаковки (SPFHP и NNLSHP) на примере Википедии (изображение автора)
Таблица 4 — Сравнение скорости работы предложенных алгоритмов упаковки (SPFHP и NNLSHP) на примере Википедии (изображение автора)
Благодаря технике векторизации накладные расходы удивительно малы, нет никаких недостатков упаковки многих последовательностей вместе.
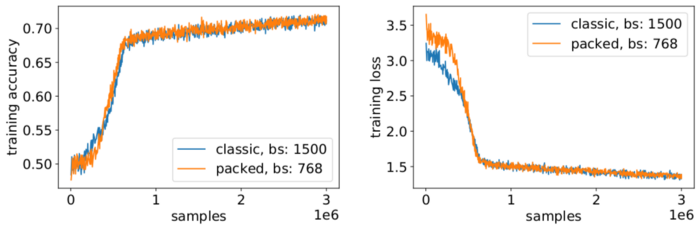 Рисунок 6 — Сравнение кривых обучения для пакетной и непакетной обработки с уменьшенным размером пакета для пакетного подхода (изображение автора)
Рисунок 6 — Сравнение кривых обучения для пакетной и непакетной обработки с уменьшенным размером пакета для пакетного подхода (изображение автора)
Точность совпадает: потеря обучения MLM может немного отличаться вначале, но быстро навёрстывается. Это первоначальное различие может быть вызвано незначительной перестройкой слоёв внимания, которые могли быть смещены в сторону коротких последовательностей в предыдущей тренировке.
Избежать замедления иногда помогает сохранение исходного размера пакета и настройка гиперпараметров на увеличенный эффективного размера пакета в 2 раза. Основными гиперпараметрами, которые необходимо рассмотреть, являются бета-параметры и скорость обучения. Одним из распространённых подходов является удвоение размера пакета, что в нашем случае снизило производительность. Глядя на статистику оптимизатора LAMB, можно доказать, что увеличение параметра бета до мощности коэффициента упаковки соответствует обучению нескольких партий подряд, чтобы импульс и скорость оставались сравнимыми.
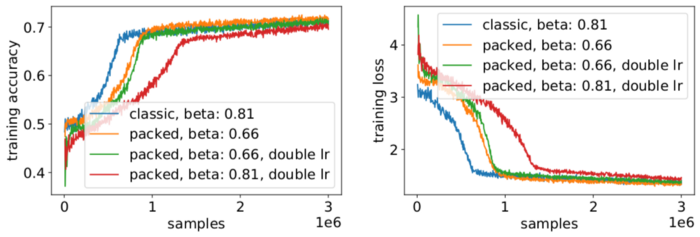 Рисунок 7 — Сравнение кривых обучения упакованной и неупакованной обработки с применением эвристики
Рисунок 7 — Сравнение кривых обучения упакованной и неупакованной обработки с применением эвристики
Наши эксперименты показали, что возведение бета в степень двойки является хорошей эвристикой. В этой ситуации ожидается, что кривые не совпадут, поскольку увеличение размера пакета обычно снижает скорость сходимости в смысле количества выборок/эпох до достижения заданной точности. Теперь вопрос в том, действительно ли в реальной ситуации мы получим ожидаемое ускорение?
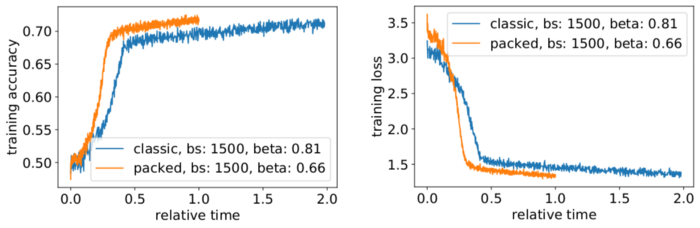 Рисунок 8 — Сравнение кривых обучения для упакованной и неупакованной обработки в **обстоятельствах оптимизации** (изображение автора)
Рисунок 8 — Сравнение кривых обучения для упакованной и неупакованной обработки в **обстоятельствах оптимизации** (изображение автора)
Да, это так! Благодаря сжатию передачи данных мы получили дополнительное ускорение.
Источник статьи: https://habr.com/ru/company/skillfactory/blog/567116/
Вычислительные потери NLP из-за заполнения последовательностей
Мы начали исследовать новые способы оптимизации обучения BERT во время работы над нашими недавними бенчмарками для MLPerf. Цель заключалась в разработке полезных оптимизаций, которые можно было бы легко использовать в реальных приложениях. BERT был естественным выбором в качестве одной из моделей для оптимизации, поскольку эта модель широко используется в промышленности, а также многими нашими клиентами.Мы очень удивились, узнав, что в нашем собственном обучающем приложении BERT-Large, использующем набор данных Wikipedia, 50 % токенов набора данных были заполнениями, что привело к большому количеству напрасных вычислений.
Заполнение последовательностей для выравнивания их длины — распространённый подход, используемый в графических процессорах, но мы решили, что стоит попробовать другой. Последовательности имеют большой разброс длины по двум причинам:
- Данные Википедии показывают большой разброс длины документов.
- Сама предварительная обработка BERT случайным образом уменьшает размер извлечённых документов, которые объединяются для создания тренировочной последовательности.

Относится ли это только к Википедии? Нет. А специфично ли явление для языка? Снова нет. На самом деле перекосы в распределении длины встречаются повсеместно: в языке, геномике и в фолдинге белков. На рисунках 2 и 3 показаны распределения в наборах данных SQuAD 1.1 и GLUE.


Как возможно работать с различными длинами, избегая при этом вычислительных потерь? Существующие подходы требуют различных вычислительных ядер для разных длин или для инженера, который должен программно удалять заполнение, а затем множество раз добавлять её обратно для каждого блока внимания и расчёта потерь. Экономия вычислений за счёт раздувания кода и его усложнения была непривлекательна, поэтому мы искали что-то лучшее.
Нельзя ли просто собрать несколько последовательностей в пакет с максимальной длиной и обработать их все вместе? Оказывается, можно! Этот подход требует трёх ключевых компонентов:
- Эффективный алгоритм принятия решения о том, какие образцы нужно сложить вместе, чтобы оставалось как можно меньше заполнения.
- Настройка модели BERT для обработки пакетов вместо последовательностей.
- Настройка гиперпараметров.
Упаковка
Сначала казалось маловероятным, что возможно очень эффективно упаковать такой большой набор данных, как Википедия. Эта проблема широко известна как задача об упаковке в контейнеры. Даже если упаковка ограничена тремя последовательностями или меньше, полученная задача всё равно будет NP-полной, то есть не имеющей эффективного алгоритмического решения. Существующие эвристические алгоритмы упаковки были неперспективны, поскольку их сложность не менее O(n log(n)), где n — количество последовательностей (~16M для Википедии). Нас интересовали подходы, которые могли бы хорошо масштабироваться на миллионы последовательностей. Значительно снизить сложность нам помогли два приёма:- Ограничение количества последовательностей в пакете до трёх (в случае первого подхода к решению).
- Работа исключительно на гистограмме длины последовательности с одним контейнером для каждой встречающейся длины.
Так почему бы не попробовать 4 последовательности в последовательности? Это увеличило количество комбинаций с 22 000 до 940 000, что было слишком много для нашего первого подхода к моделированию. Кроме того, глубина 3 уже достигла поразительно высокой эффективности. Сначала мы думали, что использование более трёх последовательностей в пакете увеличит вычислительные затраты и повлияет на сходимость во время обучения. Однако для поддержки таких приложений, как выводы, которые требуют ещё более быстрой упаковки в реальном времени, мы разработали высокоэффективный алгоритм гистограммной упаковки с неотрицательными наименьшими квадратами (NNLSHP).
Гистограммная упаковка с неотрицательными наименьшими квадратами (NNLSHP)
Упаковка контейнеров довольно часто формулируется как задача математической оптимизации. Однако при наличии 16 млн. последовательностей (или более) это нецелесообразно. Одни только переменные задачи превысили бы объём памяти большинства машин. Математическая программа подхода, основанного на гистограмме, довольно изящна. Для простоты мы выбрали подход наименьших квадратов (Ax=b) с вектором гистограммы b. Мы дополнили его, потребовав, чтобы вектор стратегий x был неотрицательным, и добавили веса, чтобы обеспечить незначительное заполнение. Самой сложной частью была матрица стратегии. Каждый её столбец имеет максимальную сумму, равную трём, и кодирует то, какие последовательности упаковываются вместе, чтобы точно соответствовать желаемой общей длине; в нашем случае это 512. Строки кодируют каждую из возможных комбинаций для достижения длины, равной общей длине. Вектор стратегии x — это то, что мы искали, он описывает, как часто выбирается любая из 20 000 комбинаций. Интересно, что в итоге было отобрано всего около 600 комбинаций. Чтобы получить точное решение, количество стратегий в x должно быть целым положительным числом, но мы поняли, что достаточно приблизительного округлённого решения с неотрицательными x. Для приближённого решения можно использовать простой готовый решатель, результат вы получите в течение 30 секунд.
В конце нам пришлось исправить некоторые образцы, которым не была назначена стратегия, но их количество было минимальным. Мы также разработали вариационный решатель, который обеспечивает упаковку каждой последовательности, потенциально с заполнением, и имеет вес, зависящий от заполнения. Это заняло гораздо больше времени, а решение оказалось ненамного лучше.
Упаковка гистограмм по кратчайшему пути
NNLSHP обеспечил нам эффективный подход к упаковке. Однако нам стало интересно, сможем ли мы теоретически получить подход быстрее с возможностью работы в режиме онлайн и снять ограничение, связанное с объединением только 3 последовательностей. Поэтому мы воспользовались существующими алгоритмами упаковки, но при этом сосредоточились на гистограммах. Наш первый алгоритм, Shortest-pack-first histogram-packing (SPFHP), состоит из четырёх ингредиентов:- Оперирование отсчётами гистограммы от самых длинных последовательностей к самым коротким.
- Если текущая длина последовательности не помещается ни в один пакет, начинается новый набор пакетов.
- Если подходит несколько, возьмите пакет, в котором сумма длин последовательностей самая короткая, и соответственно измените счётчики.
- Снова проверьте соответствие оставшихся отсчётов.

Википедия, SQuAD 1.1 и результаты упаковки GLUE
В таблицах 1–3 представлены результаты упаковки после применения двух предложенных нами алгоритмов. Глубина упаковки (packing depth) описывает максимальное количество упакованных последовательностей: 1 отражает глубину в базовой реализации BERT. Максимальная глубина упаковки, когда ограничение не установлено, обозначается дополнительным символом "max". Она описывает длину нового упакованного набора данных. Эффективность (Efficiency) — это процент реальных токенов в упакованном наборе данных. Коэффициент упаковки (packing factor) описывает результирующее потенциальное ускорение по сравнению с глубиной упаковки 1. Мы наблюдали 4 явления:- Чем больше перекос в распределении, тем больше выгода упаковки.
- От упаковки выигрывают все наборы данных, а некоторые — даже более чем в 2 раза.
- SPFHP эффективнее с неограниченной глубиной упаковки.
- Для максимального числа 3 упакованных последовательностей, чем сложнее NNLSHP, тем выше его эффективность (99,75 против 99,75. 89,44).



Настройка обработки BERT
Интересно в архитектуре BERT то, что большая часть обработки происходит на уровне токенов, а значит, обработка не мешает упаковке. В регулировке нуждаются только четыре компонента: маска внимания, потери MLM, потери NSP и точность. Ключевым моментом для всех четырёх подходов к обработке различного количества последовательностей были векторизация и использование максимального количества последовательностей, которые могут быть объединены. Для внимания у нас уже есть решающая проблему заполнения маска. Как видно из следующего псевдокода TensorFlow, расширение этого метода на несколько последовательностей было простым. Принцип следующий: мы гарантировали, что внимание ограничено отдельными последовательностями и не выйлет за их пределы. Пример кода маски внимания:mask = np.array([[1, 1, 1, 2, 2]]) # input
zero_one_mask = tf.equal(mask, mask.T) # 0, 1 mask
# for use with softmax:
softmax_mask = tf.where(zero_one_mask, 0, -1000)
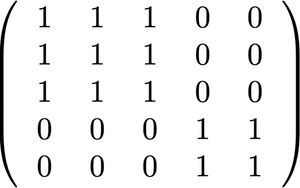
Для расчёта потерь, принципиально, последовательности распаковываются и рассчитываются потери, в итоге получаем среднее значение потерь по последовательностям (вместо пакетов). Код потерь MLM выглядит следующим образом:
# The number of sequences in each batch may vary
sequences_in_batch = tf.reduce_sum(tf.reduce_max(masked_lm_weight, -1))
sequences_in_batch = tf.cast(sequences_in_batch, tf.float32)
# Create the 0/1 mask that will be used to un-packed sequences
masked_lm_weight = tf.reshape(masked_lm_weight, [B, 1, -1])
sequence_selection = tf.reshape(tf.range(1, max_sequences_per_pack + 1), [1, -1, 1])
sequence_selection = tf.cast(masked_lm_weight == sequence_selection, tf.float32)
# Apply the mask to un-pack the loss per sequence
nll_per_token = tf.reshape(nll_per_token, [B, 1, -1])
nll_per_sequence = sequence_selection * nll_per_token
# Normalize the per-sequence loss by the number of mlm-tokens in the sequence (as is standard)
attempted = tf.reduce_sum(sequence_selection, -1, keepdims=True)
attempted = attempted + tf.cast(attempted == 0, tf.float32) # prevent NaNs when dividing by attempted
nll_per_sequence = nll_per_sequence/attempted
# Average per-batch loss (so contributions from different batches are comparable)
lm_loss = tf.reduce_sum(nll_per_sequence)/sequences_in_batch
Пример кода расчёта потерь
Для потерь NSP и точности принцип тот же. В опубликованных примерах вы найдёте соответствующий код и наш фреймворк PopART.
Оценка накладных расходов и ускорения на примере Википедии
При модификации BERT у нас возникло два вопроса:- Сколько накладных расходов она повлечёт за собой?
- Насколько сильно накладные расходы зависят от максимального количества последовательностей, которые собираются в пакет?

Благодаря технике векторизации накладные расходы удивительно малы, нет никаких недостатков упаковки многих последовательностей вместе.
Корректировки гиперпараметров
С помощью упаковки мы в среднем удваиваем эффективный размер пакета. Это означает, что нам необходимо скорректировать гиперпараметры обучения. Простой приём здесь — сократить количество накоплений градиента вдвое, чтобы сохранить тот же эффективный средний размер пакета, что и до обучения. Используя эталонную установку с предварительно обученными контрольными точками, мы видим, что кривые точности идеально совпадают.
Точность совпадает: потеря обучения MLM может немного отличаться вначале, но быстро навёрстывается. Это первоначальное различие может быть вызвано незначительной перестройкой слоёв внимания, которые могли быть смещены в сторону коротких последовательностей в предыдущей тренировке.
Избежать замедления иногда помогает сохранение исходного размера пакета и настройка гиперпараметров на увеличенный эффективного размера пакета в 2 раза. Основными гиперпараметрами, которые необходимо рассмотреть, являются бета-параметры и скорость обучения. Одним из распространённых подходов является удвоение размера пакета, что в нашем случае снизило производительность. Глядя на статистику оптимизатора LAMB, можно доказать, что увеличение параметра бета до мощности коэффициента упаковки соответствует обучению нескольких партий подряд, чтобы импульс и скорость оставались сравнимыми.

Наши эксперименты показали, что возведение бета в степень двойки является хорошей эвристикой. В этой ситуации ожидается, что кривые не совпадут, поскольку увеличение размера пакета обычно снижает скорость сходимости в смысле количества выборок/эпох до достижения заданной точности. Теперь вопрос в том, действительно ли в реальной ситуации мы получим ожидаемое ускорение?

Да, это так! Благодаря сжатию передачи данных мы получили дополнительное ускорение.
Заключение
Упаковка предложений вместе может сэкономить вычислительные ресурсы, а значит сберечь окружающую среду. Этот метод может быть реализован в любом фреймворке, включая PyTorch и TensorFlow. Мы получили явное ускорение в 2 раза и заодно дополнили работу передовым методом упаковки. Другие приложения, которые нам интересны, — это геномика и складывание белков, где можно наблюдать похожие распределения данных. Трансформеры в машинном зрении также могут стать интересной областью применения упакованных изображений разного размера.Источник статьи: https://habr.com/ru/company/skillfactory/blog/567116/
