Что-то не получаются у меня заголовки статей. Потому, что на вопрос «Как увеличить стек FPU?» очевидно же последует прямой и ясный ответ – да никак. Это же аппаратное устройство. Даже если бы и удалось увеличить его стек – тогда пришлось бы переделывать систему команд, рассчитанную на адресацию только 8 регистров ST0-ST7 Да и зачем его увеличивать? Для большинства выражений он и так очень глубокий, прямо-таки бездонный.
Стоп. Я забегаю вперед. Ведь статью могут читать и те, кто никогда не разбирался с командами процессора на низком уровне. Поэтому начну с самого начала.
Итак, FPU (Floating Point Unit) – устройство в процессоре x86 для вычислений чисел с «плавающей точкой» в формате IEEE-754. Когда-то это была отдельная микросхема 8087 с названием «сопроцессор». Работала она параллельно с основным процессором 8086 и даже была команда WAIT, которая останавливала программу и дожидалась конца выполнения очередной долгой команды сопроцессора. Я еще помню времена, когда у нас в отделе на несколько ПК был лишь один сопроцессор, мы его выковыривали отверткой и переустанавливали на тот ПК, на котором проводились большие вычисления. С появлением процессора 80486 FPU переселилось внутрь его кристалла, и проблема ушла. Кстати, команда WAIT осталась, но работает теперь не так. Впрочем, все это присказка. Главное – у FPU есть собственный магазин (стек) на восемь патронов, поэтому проводить вычисления очень удобно, а для адресации в командах FPU любого объекта в этом стеке достаточно трех бит в коде каждой такой команды.
Но на практике не всегда все проходит гладко. Допустим, я работаю в программе с числами с плавающей точкой и FPU. Я могу написать так:
X=A*B*C/D+E;
а могу вот так:
Y=A*B*C/D; X=Y+E;
Ведь результат в обоих случаях будет совершенно одинаковым, не так ли? Не совсем. Во-первых, в первом случае вычисления пройдут быстрее, поскольку не надо переписывать из стека FPU значения в переменную Y, а затем пересылать ее обратно в стек FPU при выполнении следующего оператора.
Во-вторых, даже точность вычислений может измениться. Дело в том, что FPU обеспечивает точность методом, которым обычно ловят десять тигров (для этого нужно поймать двадцать и десять отпустить). Все вычисления внутри FPU проводятся с разрядностью не 64 бит, а целых 80 бит, а при записи в 8 байт переменной типа double младшие 16 разрядов отбрасываются с округлением. Понятно, что в большинстве случаев плевать на эту ничтожную разницу, да и есть специальные команды для сохранения внутренних 80-битных значений, но факт остается фактом: в программе при работе с FPU выгоднее писать длинные выражения, а не короткие. Они и быстрее и точнее.
Вот здесь-то и могут встретиться случаи, когда глубины стека FPU для громоздкого выражения может не хватить.
В основном, это заботит разработчиков компиляторов. Над ними всегда тяготеет проклятие «общего случая». Т.е. в большинстве случаев все будет нормально, но вот в «общем случае» надо что-то делать.
А что делать в таких случаях? Например, проанализировать выражение, попытаться поменять порядок вычислений, может быть, тогда хватит стека FPU. А если в выражении есть функции, которые сами непонятно как с FPU работают? Ну, тогда, перед каждым вызовом функции нужно запоминать и потом восстанавливать состояние FPU, что очень не быстро. Ну, или, плюнуть на слишком маленький стек FPU и всегда запоминать промежуточные результаты в стеке самого процессора, что тоже, в общем, некрасиво.
Особенно сложно мне, поскольку сопровождаемый мною компилятор по сравнению с остальными даже не мини, а микро. И оптимизация там самая простая – «тактическая». С другой стороны, все-таки нужно стараться использовать стек FPU по максимуму, но, не разрабатывая для этого громоздкий оптимизатор, и не переделывая компилятор, а руководствуясь простейшими соображениями.
А соображения такие: нужно использовать «гибридный» стек, частью – процессора, а частью - FPU.
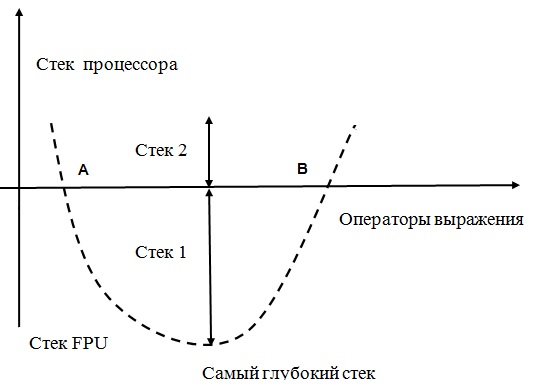
На рисунке я попытался изобразить поведение стека при вычислении очередного выражения. Изначально стек находится в нулевом положении и к нему же он приходит в конце выражения. Если бы глубины стека FPU (стек 1) хватило бы для этого выражения – все в порядке, дополнительных действий не надо. А вот если нужен стек глубже, например, стек 1 + стек 2 больше 6, тогда команды в начале выражения работают со стеком процессора, затем с точки А начинают работать уже со стеком FPU, а затем, с точки B – опять со стеком процессора. В самих точках A и B нужны две «гибридные» команды: одна берет накопленный результат из стека процессора, а свой результат помещает уже в стек FPU, а другая, наоборот, берет накопленный результат из стека FPU, но свой результат помещает уже в стек процессора. «Гибридными» команды становятся только с точки зрения остальных команд, которые обычно генерируются так, как будто стек бесконечен.
Такую, казалось бы, громоздкую схему, на самом деле легко реализовать даже в маленьком компиляторе, без серьезного анализа выражений. Главное, при этом не нужно менять генерацию самих этих выражений. В процессе генерации «нативного» кода x86 есть место, где команды FPU уже сгенерированы, но коды еще можно изменить, причем начало и конец каждого выражения известны.
В этот момент каждое выражение с уже сгенерированными командами быстро «пробегается» компилятором от конца к началу на предмет наличия команд FPU. На самом деле, мой компилятор генерирует не сами команды FPU, а «экстракоды», но логически разницы никакой. При таком просмотре выражения моделируется в простейшем виде поведение стека FPU и компилятор в своем стеке запоминает адрес этой команды, предыдущее значение стека FPU и текущее значение стека FPU. По ходу разбора определяется также максимальная глубина стека для всего выражения.
После того, как просмотр дошел до начала выражения, начинается повторный анализ, теперь уже от начала выражения к ее концу. А практически компилятор просто извлекает из своего стека адрес команды FPU и два значения стека FPU – по ним он определяет, увеличивается или уменьшается стек FPU на данной команде. Далее из максимального значения стека FPU вычитаем текущий и по этой величине определяем, можно ли уже пользоваться стеком FPU или надо еще использовать стек процессора. Поскольку направление изменения стека известно – легко находятся и сами точки A и B, где исправляются уже почти готовые коды, чтобы получилось две «гибридные» команды перехода со стека на стек.
Разберем простейший (бессмысленный и легко сокращаемый) пример, который просто заставляет мой компилятор «держать в уме» так много промежуточных вычислений, что стека FPU перестает хватать:
test roc main;
roc main;
dcl (x,x0,x1,x2,x3,x4,x5,x6,x7,x8) float(53);
x=x0/(1/x1/(1/x2/(1/x3/(1/x4/(1/x5/(1/x6/1/(1/x7/(1/x8))))))));
end test;
Компилятор сгенерировал команды, приведенные ниже. Я не буду подробно объяснять, что они делают. Напомню, что в моем микро-компиляторе особой оптимизации нет, но даже та, которая есть, выкинула некоторые лишние пересылки и сделала трудно различимыми две «гибридные» команды. По адресу в RDX находится константа 1E0 в формате IEEE-754, которая и делится на все переменные этого примера.
MOV EDX,0040A6F8
FLD64 [RBX] ; РАБОТА СО СТЕКОМ ПРОЦЕССОРА
PUSH RBX
FDIVR64 [RDX]
FST64P [RSP]
MOV EBX,0040A718 ; НАЧАЛО РАБОТЫ СО СТЕКОМ FPU
FLD64 [RBX]
FDIVR64 [RDX]
MOV EBX,0040A720
FLD64 [RBX]
FDIVR64 [RDX]
MOV EBX,0040A728
FLD64 [RBX]
FDIVR64 [RDX]
MOV EBX,0040A730
FLD64 [RBX]
FDIVR64 [RDX]
MOV EBX,0040A738
FLD64 [RBX]
FDIVR64 [RDX]
MOV EBX,0040A6F8
FDIV64 [RBX]
MOV EBX,0040A740
FLD64 [RBX]
FDIVR64 [RDX]
MOV EBX,0040A748
FLD64 [RBX]
FDIVR64 [RDX]
FDIVP ST1,ST
FDIVP ST1,ST
FDIVP ST1,ST
FDIVP ST1,ST
FDIVP ST1,ST
FDIVP ST1,ST ; ОКОНЧАНИЕ РАБОТЫ СО СТЕКОМ FPU
FDIVR64 [RSP] ; ОПЯТЬ РАБОТА СО СТЕКОМ ПРОЦЕССОРА
MOV EBX,0040A708
FDIVR64 [RBX]
POP RAX
FST64P [0040A700] .X ; ЗАПИСЬ ОТВЕТА В ПЕРЕМЕННУЮ X
Таким образом, применив несложную доработку компилятора при обработке сгенерированных команд, удалось решить задачу максимального использования стека FPU в общем случае сложного выражения. В чем-то это даже похоже на увеличение стека FPU таким вот виртуальным способом, поскольку разбор выражения в компиляторе остался прежним, как бы считающим стек бесконечным.
Правда, если в выражении встречаются не встроенные (и даже некоторые встроенные) функции, от использования стека FPU в таких выражениях приходится отказываться.
P.S. Во времена, когда FPU еще была отдельной микросхемой, одна из фирм, производящих сопроцессоры, предложила оригинальное решение: в ее микросхеме было сразу несколько стеков и можно было переключаться между ними специальной командой. На мой взгляд, очень хорошее решение, тоже, по сути, увеличивающее стек FPU. Ведь заполнив один стек, я тогда мог переключиться на следующий еще свободный. Почему-то в современных процессорах с их миллиардами транзисторов, которые не знают подо что еще занять, подобные решения не применяются.

 habr.com
habr.com
Стоп. Я забегаю вперед. Ведь статью могут читать и те, кто никогда не разбирался с командами процессора на низком уровне. Поэтому начну с самого начала.
Итак, FPU (Floating Point Unit) – устройство в процессоре x86 для вычислений чисел с «плавающей точкой» в формате IEEE-754. Когда-то это была отдельная микросхема 8087 с названием «сопроцессор». Работала она параллельно с основным процессором 8086 и даже была команда WAIT, которая останавливала программу и дожидалась конца выполнения очередной долгой команды сопроцессора. Я еще помню времена, когда у нас в отделе на несколько ПК был лишь один сопроцессор, мы его выковыривали отверткой и переустанавливали на тот ПК, на котором проводились большие вычисления. С появлением процессора 80486 FPU переселилось внутрь его кристалла, и проблема ушла. Кстати, команда WAIT осталась, но работает теперь не так. Впрочем, все это присказка. Главное – у FPU есть собственный магазин (стек) на восемь патронов, поэтому проводить вычисления очень удобно, а для адресации в командах FPU любого объекта в этом стеке достаточно трех бит в коде каждой такой команды.
Но на практике не всегда все проходит гладко. Допустим, я работаю в программе с числами с плавающей точкой и FPU. Я могу написать так:
X=A*B*C/D+E;
а могу вот так:
Y=A*B*C/D; X=Y+E;
Ведь результат в обоих случаях будет совершенно одинаковым, не так ли? Не совсем. Во-первых, в первом случае вычисления пройдут быстрее, поскольку не надо переписывать из стека FPU значения в переменную Y, а затем пересылать ее обратно в стек FPU при выполнении следующего оператора.
Во-вторых, даже точность вычислений может измениться. Дело в том, что FPU обеспечивает точность методом, которым обычно ловят десять тигров (для этого нужно поймать двадцать и десять отпустить). Все вычисления внутри FPU проводятся с разрядностью не 64 бит, а целых 80 бит, а при записи в 8 байт переменной типа double младшие 16 разрядов отбрасываются с округлением. Понятно, что в большинстве случаев плевать на эту ничтожную разницу, да и есть специальные команды для сохранения внутренних 80-битных значений, но факт остается фактом: в программе при работе с FPU выгоднее писать длинные выражения, а не короткие. Они и быстрее и точнее.
Вот здесь-то и могут встретиться случаи, когда глубины стека FPU для громоздкого выражения может не хватить.
В основном, это заботит разработчиков компиляторов. Над ними всегда тяготеет проклятие «общего случая». Т.е. в большинстве случаев все будет нормально, но вот в «общем случае» надо что-то делать.
А что делать в таких случаях? Например, проанализировать выражение, попытаться поменять порядок вычислений, может быть, тогда хватит стека FPU. А если в выражении есть функции, которые сами непонятно как с FPU работают? Ну, тогда, перед каждым вызовом функции нужно запоминать и потом восстанавливать состояние FPU, что очень не быстро. Ну, или, плюнуть на слишком маленький стек FPU и всегда запоминать промежуточные результаты в стеке самого процессора, что тоже, в общем, некрасиво.
Особенно сложно мне, поскольку сопровождаемый мною компилятор по сравнению с остальными даже не мини, а микро. И оптимизация там самая простая – «тактическая». С другой стороны, все-таки нужно стараться использовать стек FPU по максимуму, но, не разрабатывая для этого громоздкий оптимизатор, и не переделывая компилятор, а руководствуясь простейшими соображениями.
А соображения такие: нужно использовать «гибридный» стек, частью – процессора, а частью - FPU.
На рисунке я попытался изобразить поведение стека при вычислении очередного выражения. Изначально стек находится в нулевом положении и к нему же он приходит в конце выражения. Если бы глубины стека FPU (стек 1) хватило бы для этого выражения – все в порядке, дополнительных действий не надо. А вот если нужен стек глубже, например, стек 1 + стек 2 больше 6, тогда команды в начале выражения работают со стеком процессора, затем с точки А начинают работать уже со стеком FPU, а затем, с точки B – опять со стеком процессора. В самих точках A и B нужны две «гибридные» команды: одна берет накопленный результат из стека процессора, а свой результат помещает уже в стек FPU, а другая, наоборот, берет накопленный результат из стека FPU, но свой результат помещает уже в стек процессора. «Гибридными» команды становятся только с точки зрения остальных команд, которые обычно генерируются так, как будто стек бесконечен.
Такую, казалось бы, громоздкую схему, на самом деле легко реализовать даже в маленьком компиляторе, без серьезного анализа выражений. Главное, при этом не нужно менять генерацию самих этих выражений. В процессе генерации «нативного» кода x86 есть место, где команды FPU уже сгенерированы, но коды еще можно изменить, причем начало и конец каждого выражения известны.
В этот момент каждое выражение с уже сгенерированными командами быстро «пробегается» компилятором от конца к началу на предмет наличия команд FPU. На самом деле, мой компилятор генерирует не сами команды FPU, а «экстракоды», но логически разницы никакой. При таком просмотре выражения моделируется в простейшем виде поведение стека FPU и компилятор в своем стеке запоминает адрес этой команды, предыдущее значение стека FPU и текущее значение стека FPU. По ходу разбора определяется также максимальная глубина стека для всего выражения.
После того, как просмотр дошел до начала выражения, начинается повторный анализ, теперь уже от начала выражения к ее концу. А практически компилятор просто извлекает из своего стека адрес команды FPU и два значения стека FPU – по ним он определяет, увеличивается или уменьшается стек FPU на данной команде. Далее из максимального значения стека FPU вычитаем текущий и по этой величине определяем, можно ли уже пользоваться стеком FPU или надо еще использовать стек процессора. Поскольку направление изменения стека известно – легко находятся и сами точки A и B, где исправляются уже почти готовые коды, чтобы получилось две «гибридные» команды перехода со стека на стек.
Разберем простейший (бессмысленный и легко сокращаемый) пример, который просто заставляет мой компилятор «держать в уме» так много промежуточных вычислений, что стека FPU перестает хватать:
test
dcl (x,x0,x1,x2,x3,x4,x5,x6,x7,x8) float(53);
x=x0/(1/x1/(1/x2/(1/x3/(1/x4/(1/x5/(1/x6/1/(1/x7/(1/x8))))))));
end test;
Компилятор сгенерировал команды, приведенные ниже. Я не буду подробно объяснять, что они делают. Напомню, что в моем микро-компиляторе особой оптимизации нет, но даже та, которая есть, выкинула некоторые лишние пересылки и сделала трудно различимыми две «гибридные» команды. По адресу в RDX находится константа 1E0 в формате IEEE-754, которая и делится на все переменные этого примера.
MOV EDX,0040A6F8
FLD64 [RBX] ; РАБОТА СО СТЕКОМ ПРОЦЕССОРА
PUSH RBX
FDIVR64 [RDX]
FST64P [RSP]
MOV EBX,0040A718 ; НАЧАЛО РАБОТЫ СО СТЕКОМ FPU
FLD64 [RBX]
FDIVR64 [RDX]
MOV EBX,0040A720
FLD64 [RBX]
FDIVR64 [RDX]
MOV EBX,0040A728
FLD64 [RBX]
FDIVR64 [RDX]
MOV EBX,0040A730
FLD64 [RBX]
FDIVR64 [RDX]
MOV EBX,0040A738
FLD64 [RBX]
FDIVR64 [RDX]
MOV EBX,0040A6F8
FDIV64 [RBX]
MOV EBX,0040A740
FLD64 [RBX]
FDIVR64 [RDX]
MOV EBX,0040A748
FLD64 [RBX]
FDIVR64 [RDX]
FDIVP ST1,ST
FDIVP ST1,ST
FDIVP ST1,ST
FDIVP ST1,ST
FDIVP ST1,ST
FDIVP ST1,ST ; ОКОНЧАНИЕ РАБОТЫ СО СТЕКОМ FPU
FDIVR64 [RSP] ; ОПЯТЬ РАБОТА СО СТЕКОМ ПРОЦЕССОРА
MOV EBX,0040A708
FDIVR64 [RBX]
POP RAX
FST64P [0040A700] .X ; ЗАПИСЬ ОТВЕТА В ПЕРЕМЕННУЮ X
Таким образом, применив несложную доработку компилятора при обработке сгенерированных команд, удалось решить задачу максимального использования стека FPU в общем случае сложного выражения. В чем-то это даже похоже на увеличение стека FPU таким вот виртуальным способом, поскольку разбор выражения в компиляторе остался прежним, как бы считающим стек бесконечным.
Правда, если в выражении встречаются не встроенные (и даже некоторые встроенные) функции, от использования стека FPU в таких выражениях приходится отказываться.
P.S. Во времена, когда FPU еще была отдельной микросхемой, одна из фирм, производящих сопроцессоры, предложила оригинальное решение: в ее микросхеме было сразу несколько стеков и можно было переключаться между ними специальной командой. На мой взгляд, очень хорошее решение, тоже, по сути, увеличивающее стек FPU. Ведь заполнив один стек, я тогда мог переключиться на следующий еще свободный. Почему-то в современных процессорах с их миллиардами транзисторов, которые не знают подо что еще занять, подобные решения не применяются.
Как увеличить стек FPU
Что-то не получаются у меня заголовки статей. Потому, что на вопрос «Как увеличить стек FPU?» очевидно же последует прямой и ясный ответ – да никак. Это же аппаратное устройство. Даже если бы и...
