О бедном бите замолвите слово

Kate · 18 Дек 2021

Постановка задачи

В компании X происходит очередной ребрендинг. Пригласили дорогостоящих спецов, они выкатили на общественное голосование 6 вариантов логотипов. Тут и «стремительная I» и «бесконечно многогранная O» и «гибкая W» и «строгий графит» и «веселый лайм»...

Собрали с сотрудников ответы, каждый должен был написать набор чисел из множества [1; 6], соответствующих понравившимся логотипам. Некоторые были четко уверены и указали только один вариант. Другие занимали различные точки зрения и указали все 6. Третьи выбрали умеренность и указали что-то посерединке.

Получили мы на вход примерно такой набор данных по которому надо выбрать самый популярный логотип.

uid vote
1: id001 6,5,3
2: id002 5,3,4,2,1
3: id003 2,5,4,3
4: id004 1,4
5: id005 2,3,5,1
6: id006 3
7: id007 6,3
8: id008 2,5,6,4,3

Задача простая, решается миллионом разных способов. Но попробуем немного добавить в нее разнообразия.

Вариант 1

Классический выпускник DS курсов предложит все это преобразовать в прямоугольную таблицу и потом, возможно путем pivot преобразований, посчитать различные отношения. Засада в неквадратности данных, но это вполне обходимо.

На выходе может получиться примерно такой код:

library(tidyverse)

# эмулируем данные
df <- tibble(
id = 1:3,
answer_1 = rep(1, 3),
answer_2 = rep(2, 3),
answer_3 = c(3, NA, NA),
answer_4 = c(4, NA, 4),
answer_5 = rep(5, 3),
answer_6 = rep(6, 3)
)

df %>%
pivot_longer(-id, names_to = NULL, values_to = "brand_id") %>%
filter(!is.na(brand_id)) %>%
group_by(id) %>%
summarise(
recognized_brands = list(brand_id),
unrecognized_brands = map(recognized_brands, function(x) setdiff(x = 1:6, y= x))
) %>%
unnest_longer(recognized_brands) %>%
unnest_longer(unrecognized_brands) %>%
pivot_longer(-id, names_to = "type", values_to = "brand_id") %>%
filter(!is.na(brand_id)) %>%
distinct() %>%
group_by(brand_id, type) %>%
summarise(N = n()) %>%
pivot_wider(names_from = type, values_from = N, values_fill = 0) %>%
mutate(brand_recognition = recognized_brands / (recognized_brands + unrecognized_brands))

Получаем примерно такой ответ:

# A tibble: 6 x 4
# Groups: brand_id [6]
brand_id recognized_brands unrecognized_brands brand_recognition
<dbl> <int> <int> <dbl>
1 1 3 0 1
2 2 3 0 1
3 3 1 2 0.333
4 4 2 1 0.667
5 5 3 0 1
6 6 3 0 1

Неплохо, результат получен. Чего еще хотеть?

Вариант 2

Если нас никак не интересуют показатели в разрезе отдельных сотрудников, то мы можем поступить чуть проще. Свалим все в кучу и в ней же посчитаем.

Прямо Спортлото какое-то. Куча шаров и 6 цифр.

library(tidyverse)

# подготовим тестовые данные =============
df <- tibble(uid = sprintf("id%03d", 1:100)) %>%
rowwise() %>%
mutate(vote = list(sample(1:6, runif(1, 1, 6)))) %>%
ungroup()

# расчеты
unlist(df$vote) %>%
janitor::tabyl()

Получаем ответ в одну строчку

. n percent
1 54 0.1703470
2 55 0.1735016
3 52 0.1640379
4 52 0.1640379
5 52 0.1640379
6 52 0.1640379

Вариант 3

Предположим, что нам будет важна исходная таблица по распределению ответов каждого сотрудника в Excel. Т.е. все эти циферки 1..6 надо разнести по 6-ти колонкам. Вариант 1 мы уже имеем с преобразованиями из длинного в широкое и наоборот.

Но есть и другой веселый способ. Используем его, чтобы поговорить про биты и двоичную систему счисления.

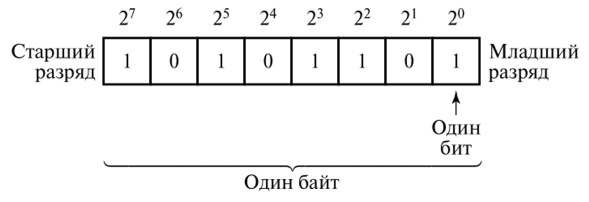
Что есть таблица ответов? По сути, это матрица с 0 и 1, где колонки соответствуют номеру логотипа, а строчки — мнению каждого отдельного сотрудника. Если ответ бинарен, а позиций всего 6, то у нас есть прекрасная возможность использовать двоичное представление чисел для кодирования ответов.

Не будем морочиться с сопоставлением номеров ответов с соответствующими колонками, не будем заниматься сортировкой ответов. За нас все сделает машина.

Просто скомпонуем числа, размещая 1 в тех битах, которые соотв. заполненным номерам. Делаем это с помощью суммы степеней двойки (см. картинку). Дальше можно провести битовые векторизированные вычисления с применением AND по соответствующему разряду, сдвигу вправо или же можем просто преобразовать в матрицу.

library(tidyverse)
library(bitops)

# подготовим тестовые данные =============
df <- tibble(uid = sprintf("id%03d", 1:100)) %>%
rowwise() %>%
mutate(vote = list(sample(1:6, runif(1, 1, 6)))) %>%
ungroup()

# решаем задачу =============
# конструируем битовую маску ответов для каждого человека
res_df <- df %>%
rowwise() %>%
mutate(mask = sum(2^vote),
logo = matrix(
as.logical(bitAnd(mask, c(1, 2, 4, 8, 16, 32))),
nrow = 1)
) %>%
ungroup()

# матрицу преобразуем в целочисленную
mm <- res_df$logo * 1L

sum(mm)
# считаем по колонкам
colMeans(mm)
colSums(mm)

Заключение

Грузить и трансформировать Большие Данные — важная и нужная задача. Но если вспоминать про базовые вещи, то иногда задачи можно решать веселее и экономнее. И иногда спускаться из облаков и петабайтов и вспоминать про существование битов.