Вокруг нас появляется все больше различных устройств, систем, комплексов, платформ – технологических, информационных, киберфизических. Мы не задумываемся о том, как кофеварка варит кофе, робот-пылесос выбирает маршрут при уборке квартиры, система биометрической идентификации определяет человека на видеокадре, а портал государственных услуг обрабатывает наше заявление на получение справки об отсутствии судимости. Мы привыкаем к этим системам как к «черным ящикам», которые дают предсказуемый результат на выходе, не заботясь о том, как эти системы себя «чувствуют». Такой потребительский подход простителен пользователям, но совсем по-другому относятся к этому компании-разработчики и те, кто занимается эксплуатацией технологических систем. Для них и описан далее один из оригинальных методов поиска аномалий во временных рядах, т.е. состояний, по которым можно понять, что системе становится «плохо» (либо станет в ближайшем будущем).
Для эффективной эксплуатации сложных технологических систем нужны мониторинг и различные методы аналитики, позволяющие контролировать, управлять, упреждающе менять параметры. Мониторинг, как правило, обеспечивается типовыми инструментами (в большинстве случаев достаточно надежной системы сбора и визуализации данных). А вот для создания эффективных аналитических инструментов необходимы дополнительные исследования, эксперименты и хорошее знание предметной области. Как правило выделяют четыре основных вида аналитики данных [1]:
Сфер применения инструментов аналитики очень много - информационная безопасность, банковский сектор, государственное управление, медицина и многие другие предметные области. Часто один и тот же метод эффективно работает для разных предметных областей, поэтому разработчики систем аналитики создают универсальные модули, содержащие различные алгоритмы.
Для многих технологических систем результаты мониторинга можно представить в виде временных рядов [2]. Свойствами временного ряда являются:
Рис. 1. Временной ряд
Временные ряды могут описывать не только численно измеримые процессы. Применение различных методов и архитектур моделей, включая глубокие нейронные сети, позволяет работать с данными из задач обработки естественного языка (NLP), компьютерного зрения (CV) и т.п. Например, сообщения в чате можно преобразовать в числовые векторы (эмбеддинги), которые последовательно появляются в определенное время, а видео представляет из себя ни что иное как матрицу чисел, изменяющуюся во времени.
Итак, временные ряды очень полезны для описания работы сложных устройств и часто используются для типовых задач: моделирование, прогнозирование, выделение признаков, классификация, кластеризация, поиск паттернов, поиск аномалий. Примеры такого использования: электрокардиограмма, изменение стоимости акций или валюты, значения прогноза погоды, изменение в объеме сетевого трафика, параметры работы двигателя и многое другое.
Рис.2. Практические примеры временных рядов: электрокардиограмма, прогноз погоды.
У временных рядов есть типовые характеристики, которые достаточно точно описывают характер временного ряда:
Точечные аномалии распознаются проще всего – это отдельные точки, в которых поведение процесса резко отличается от других точек. Например, можно наблюдать резкое отклонение значений параметра в отдельной точке.
Рис.3. Несколько точечных аномалий.
Такие значения называются «выбросы», они сильно влияют на статистические показатели процесса и их легко обнаружить, установив пороговые значения для наблюдаемой величины.
Сложнее обнаружить аномалию в ситуации, когда в каждой точке процесс ведет себя «нормально», но в совокупности значения в нескольких точках ведут себя «странно». К такому аномальному поведению можно отнести, например, изменение формы сигнала, изменение статистических показателей (среднее значение, мода, медиана, дисперсия), появление взаимной корреляции между двумя параметрами, небольшие или краткосрочные аномальные изменения амплитуды и так далее. И в этом случае задача заключается в распознавании аномального поведения параметров, которое нельзя выявить обычными статистическими методами.
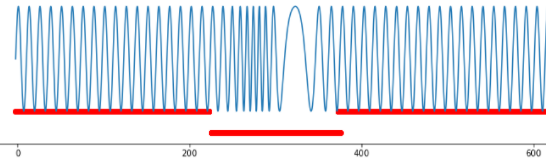Рис.4. Групповая аномалия, изменение частоты.
Поиск аномалий очень важен. В одной ситуации надо данные очищать от аномалий, чтобы получать более реальную картину, в другой же ситуации аномалии должны внимательно исследоваться, так как могут свидетельствовать о возможном скором переходе устройства в аварийный режим.
Поиск аномалий во временных рядах непрост (нечеткое определение аномалии, отсутствие разметки, неочевидная корреляция). До сих пор SOTA алгоритмы по поиску аномалий во временных рядах имеют высокий уровень False Positive.
Вручную можно обнаружить только небольшое количество аномалий, в основном точечных, при наличии хорошей визуализации данных. Групповые аномалии сложнее обнаружить вручную, особенно если речь идет о большом количестве данных и анализе информации о нескольких устройствах. Также сложным для выявления является случай «аномалии во времени», когда нормальный по параметрам сигнал появляется в «неправильное» время. Поэтому при поиске аномалий во временных рядах целесообразно применять методы автоматизации.
Большой проблемой в поиске аномалий на реальных данных является то, что данные как правило не размечены, поэтому изначально строго не определено, что такое аномалия, нет правил для поиска. В таких ситуациях необходимо применять методы обучения без учителя (unsupervised learning), при этом модели самостоятельно определяют взаимосвязи и характерные законы в данных.
Используемые для поиска аномалий во временных рядах методы принято разделять на группы [3]:
В prediction-based методах основная задача – построить качественную модель процесса, чтобы смоделировать сигнал и сравнить полученные смоделированные значения с исходными (истинными). Если предсказанный и истинный сигнал близки, то поведение считается «нормальным», а если значения в модели сильно отличаются от истинных, то поведение системы на этом участке объявляется аномальным.
Рис.5. Моделирование временного ряда.
Наиболее распространенные методы для моделирования временных рядов – SARIMA [4] и рекуррентные нейронные сети [5].
Оригинальный подход используется в reconstruction-based моделях – сначала модель обучают кодировать и декодировать сигналы из имеющейся выборки, при этом закодированный сигнал имеет гораздо меньшую размерность, чем исходный, поэтому модели приходится учиться «сжимать» информацию. Вот пример такого сжатия для картинок 32 на 32 пикселя в матрицу из 32 чисел.
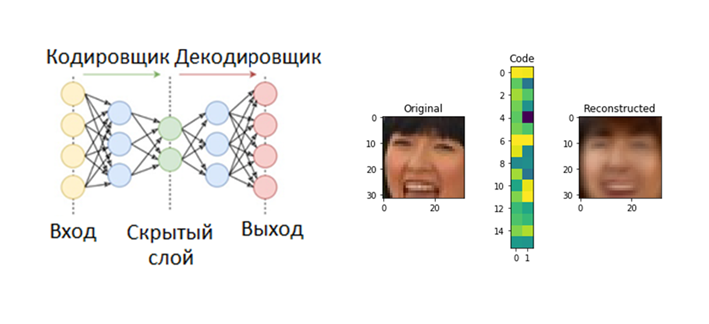Рис.6. Схема работы автокодировщика
После обучения модели дают на вход сигналы, являющиеся отрезками исследуемого временного ряда, и если кодирование-декодирование проходит успешно, то поведение процесса считается «нормальным», в противном случае поведение объявляется аномальным.
Одним из недавно разработанных reconstruction-based методов, показывающих хорошие результаты в обнаружении аномалий, является TadGAN [3], разработанный исследователями из MIT в конце 2020 года. Архитектура метода TadGAN содержит в себе элементы актокодировщика и генеративных состязательных сетей.
![Рис.7. Архитектура TadGAN (из статьи [3])](https://habrastorage.org/r/w1560/getpro/habr/upload_files/507/197/d04/507197d04b43daa9e8ff8441a284096d.png "Рис.7. Архитектура TadGAN (из статьи [3])")
Рис.7. Архитектура TadGAN (из статьи [3])
Ɛ действует как кодировщик, переводящий отрезки временных рядов x в векторы скрытого пространства z, а G – декодер, восстанавливающий из скрытого представления z отрезки временных рядов. Cx – критик, оценивающий качество восстановления G(Ɛ(х)). Кроме того, действует контроль «похожести» исходного и восстановленного сэмплов с использованием L2 - меры по идеологии «Cycle consistency loss» (обеспечивает общую похожесть сгенерированных образцов на исходные сэмплы в GAN) [6]. Итоговая целевая функция - объединение всех метрик для оценки качества работы критиков Cx, Cz и меры похожести исходного и восстановленного сигнала.
Для создания и обучения нейронной сети могут быть использованы различные стандартные пакеты (например, TensorFlow или PyTorch), имеющие высокоуровневое API. Пример реализации архитектуры, аналогичной TadGAN, с использованием пакета TensorFlow для обучения весов можно посмотреть в репозитории [7]. При обучении этой модели оптимизировались пять метрик:
Рис.8. График обучения модели TadGAN для 500 эпох.
После обучения модели проводится реконструкция отдельных отрезков исследуемого временного ряда и сравнение исходного и реконструированного ряда, которое может осуществляться одним из методов:
Для демонстрации работы метода используем синтетический (искусственно сгенерированный) ряд без аномалий, являющийся суммой двух синусоид, значения которого меняются в диапазоне от -1 до 1
График этого ряда:
Рис.9. График синтетического ряда.
Восстановленный ряд с использованием TadGAN для разного количества эпох (4 и 80) выглядит так:
Рис.10. Моделирование ряда с помощью TadGAN для разного количества эпох (4 и 80)
Видно, что модель достаточно точно научилась предсказывать основные закономерности в данных. Попробуем добавить различные аномалии в данных и затем обнаружить их с помощью модели TadGAN. Сначала добавим несколько точечных аномалий.
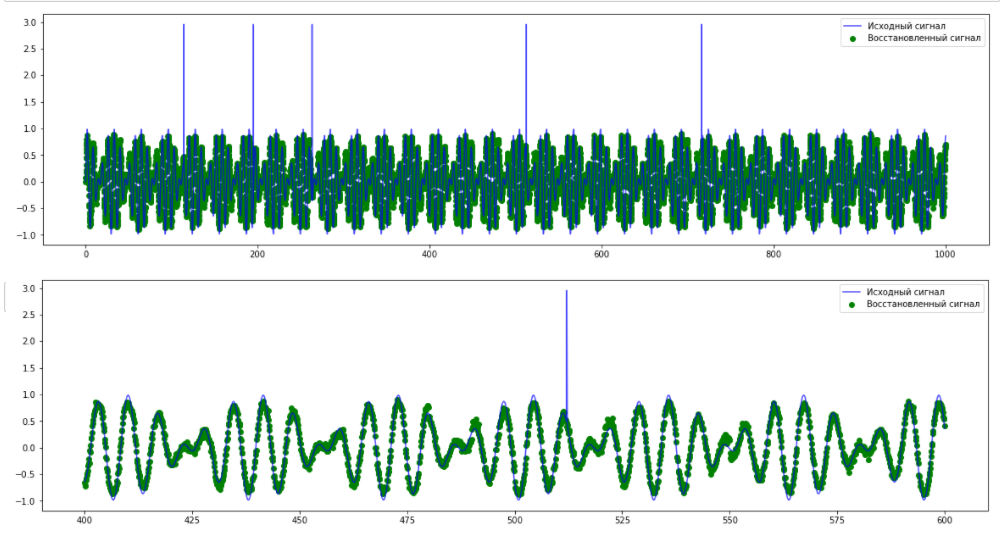Рис.11. Обнаружение точечной аномалии с помощью TadGAN
Из графика исходного и предсказанного сигналов видно, что модель не может восстановить «пики» аномальных значений, что с высокой точностью может использоваться для определения точечных аномалий. Однако в такой ситуации польза сложной модели TadGAN неочевидна – подобные аномалии можно обнаружить и с помощью оценки превышения пороговых значений.
Теперь рассмотрим сигнал с другим типом аномалии - периодический сигнал с аномальным изменением частоты. В этом случае нет превышения порога – с точки зрения амплитуды все элементы ряда являются «нормальными» значениями, и аномалия выявляется только в групповом поведении нескольких точек. В этом случае TadGAN также не может восстановить сигнал (как это видно на рисунке) и это может быть использовано в качестве признака наличия групповой аномалии.
Рис.12. Результат работы TadGAN на датасете с аномальным изменением частоты.
На этих двух примерах проиллюстрирована работа метода. Читатель и сам может попробовать создать свои датасеты и проверить возможности модели в различных ситуациях.
Более сложные примеры датасетов можно найти в статье авторов метода TadGAN [3]. Там же приведена ссылка на библиотеку Orion, являющуюся разработкой специалистов MIT, которая с использованием машинного обучения распознает редкие аномалии во временных рядах, используя подход обучения без учителя (unsupervised learning).
В заключении отметим, что методов, использующих реконструирование сигнала (reconstruction-based) для обнаружения аномалии сейчас очень много, например в ресурсе arxiv.org десятки статей, описывающих различные модификации подхода с использованием автокодировщиков и генеративных состязательных сетей. Для каждой конкретной задачи целесообразно подбирать свою модель, с учетом требований задачи и знаний о предметной области.
habr.com
Для эффективной эксплуатации сложных технологических систем нужны мониторинг и различные методы аналитики, позволяющие контролировать, управлять, упреждающе менять параметры. Мониторинг, как правило, обеспечивается типовыми инструментами (в большинстве случаев достаточно надежной системы сбора и визуализации данных). А вот для создания эффективных аналитических инструментов необходимы дополнительные исследования, эксперименты и хорошее знание предметной области. Как правило выделяют четыре основных вида аналитики данных [1]:
- Описательная аналитика визуализирует накопленные данные, в том числе преобразованные для наглядности и интерпретируемости. Описательная аналитика - самый простой вид анализа, но и самый важный для применения других методов анализа.
- С помощью диагностической аналитики исследуют причину возникновения событий в прошлом, при этом выявляются тренды, аномалии, наиболее характерные черты описываемого процесса, ищут причины и корреляции (взаимосвязи).
- Прогнозная аналитика предсказывает вероятные результаты на основе выявленных тенденций и статистических моделей, полученных с помощью исторических данных.
- Предписывающая аналитика позволяет получить оптимальное решение производственной задачи на основе прогнозной аналитики. Например, это может быть оптимизация параметров работы оборудования или бизнес-процессов, перечень мер по предотвращению аварийной ситуации.
Сфер применения инструментов аналитики очень много - информационная безопасность, банковский сектор, государственное управление, медицина и многие другие предметные области. Часто один и тот же метод эффективно работает для разных предметных областей, поэтому разработчики систем аналитики создают универсальные модули, содержащие различные алгоритмы.
Для многих технологических систем результаты мониторинга можно представить в виде временных рядов [2]. Свойствами временного ряда являются:
- привязка каждого измерения (сэмпла, дискрета) ко времени его возникновения,
- равное расстояние по времени между измерениями,
- возможность из данных предыдущего периода восстановить поведение процесса в текущем и последующих периодах.
Временные ряды могут описывать не только численно измеримые процессы. Применение различных методов и архитектур моделей, включая глубокие нейронные сети, позволяет работать с данными из задач обработки естественного языка (NLP), компьютерного зрения (CV) и т.п. Например, сообщения в чате можно преобразовать в числовые векторы (эмбеддинги), которые последовательно появляются в определенное время, а видео представляет из себя ни что иное как матрицу чисел, изменяющуюся во времени.
Итак, временные ряды очень полезны для описания работы сложных устройств и часто используются для типовых задач: моделирование, прогнозирование, выделение признаков, классификация, кластеризация, поиск паттернов, поиск аномалий. Примеры такого использования: электрокардиограмма, изменение стоимости акций или валюты, значения прогноза погоды, изменение в объеме сетевого трафика, параметры работы двигателя и многое другое.
У временных рядов есть типовые характеристики, которые достаточно точно описывают характер временного ряда:
- период - временной отрезок постоянной для всего ряда длины, на концах которого ряд принимает близкие значения,
- сезонность - свойство периодичности (сезон=период),
- цикл - характерные изменения ряда, связанные с глобальными причинами (например, циклы в экономике), нет постоянного периода,
- тренд - тенденция к долгосрочному увеличению или уменьшению значений ряда.
Точечные аномалии распознаются проще всего – это отдельные точки, в которых поведение процесса резко отличается от других точек. Например, можно наблюдать резкое отклонение значений параметра в отдельной точке.
Такие значения называются «выбросы», они сильно влияют на статистические показатели процесса и их легко обнаружить, установив пороговые значения для наблюдаемой величины.
Сложнее обнаружить аномалию в ситуации, когда в каждой точке процесс ведет себя «нормально», но в совокупности значения в нескольких точках ведут себя «странно». К такому аномальному поведению можно отнести, например, изменение формы сигнала, изменение статистических показателей (среднее значение, мода, медиана, дисперсия), появление взаимной корреляции между двумя параметрами, небольшие или краткосрочные аномальные изменения амплитуды и так далее. И в этом случае задача заключается в распознавании аномального поведения параметров, которое нельзя выявить обычными статистическими методами.
Поиск аномалий очень важен. В одной ситуации надо данные очищать от аномалий, чтобы получать более реальную картину, в другой же ситуации аномалии должны внимательно исследоваться, так как могут свидетельствовать о возможном скором переходе устройства в аварийный режим.
Поиск аномалий во временных рядах непрост (нечеткое определение аномалии, отсутствие разметки, неочевидная корреляция). До сих пор SOTA алгоритмы по поиску аномалий во временных рядах имеют высокий уровень False Positive.
Вручную можно обнаружить только небольшое количество аномалий, в основном точечных, при наличии хорошей визуализации данных. Групповые аномалии сложнее обнаружить вручную, особенно если речь идет о большом количестве данных и анализе информации о нескольких устройствах. Также сложным для выявления является случай «аномалии во времени», когда нормальный по параметрам сигнал появляется в «неправильное» время. Поэтому при поиске аномалий во временных рядах целесообразно применять методы автоматизации.
Большой проблемой в поиске аномалий на реальных данных является то, что данные как правило не размечены, поэтому изначально строго не определено, что такое аномалия, нет правил для поиска. В таких ситуациях необходимо применять методы обучения без учителя (unsupervised learning), при этом модели самостоятельно определяют взаимосвязи и характерные законы в данных.
Используемые для поиска аномалий во временных рядах методы принято разделять на группы [3]:
- proximity-based: выявление аномалии на основе информации о близости параметров или последовательности параметров фиксированной длины, подходит для выявления точечных аномалий и выбросов, но не позволит выявить изменения в форме сигнала,
- prediction-based: построение прогнозной модели и сравнение прогноза и фактической величины, лучше всего применимо ко временным рядам с выраженными периодами, циклами или сезонностью,
- reconstruction-based: методы, основанные на реконструкции фрагментов данных, используют восстановление (реконструкцию) фрагмента данных, поэтому может выявлять как точечные аномалии, так и групповые аномалии, в том числе изменения в форме сигнала.
В prediction-based методах основная задача – построить качественную модель процесса, чтобы смоделировать сигнал и сравнить полученные смоделированные значения с исходными (истинными). Если предсказанный и истинный сигнал близки, то поведение считается «нормальным», а если значения в модели сильно отличаются от истинных, то поведение системы на этом участке объявляется аномальным.
Наиболее распространенные методы для моделирования временных рядов – SARIMA [4] и рекуррентные нейронные сети [5].
Оригинальный подход используется в reconstruction-based моделях – сначала модель обучают кодировать и декодировать сигналы из имеющейся выборки, при этом закодированный сигнал имеет гораздо меньшую размерность, чем исходный, поэтому модели приходится учиться «сжимать» информацию. Вот пример такого сжатия для картинок 32 на 32 пикселя в матрицу из 32 чисел.
После обучения модели дают на вход сигналы, являющиеся отрезками исследуемого временного ряда, и если кодирование-декодирование проходит успешно, то поведение процесса считается «нормальным», в противном случае поведение объявляется аномальным.
Одним из недавно разработанных reconstruction-based методов, показывающих хорошие результаты в обнаружении аномалий, является TadGAN [3], разработанный исследователями из MIT в конце 2020 года. Архитектура метода TadGAN содержит в себе элементы актокодировщика и генеративных состязательных сетей.
Ɛ действует как кодировщик, переводящий отрезки временных рядов x в векторы скрытого пространства z, а G – декодер, восстанавливающий из скрытого представления z отрезки временных рядов. Cx – критик, оценивающий качество восстановления G(Ɛ(х)). Кроме того, действует контроль «похожести» исходного и восстановленного сэмплов с использованием L2 - меры по идеологии «Cycle consistency loss» (обеспечивает общую похожесть сгенерированных образцов на исходные сэмплы в GAN) [6]. Итоговая целевая функция - объединение всех метрик для оценки качества работы критиков Cx, Cz и меры похожести исходного и восстановленного сигнала.
Для создания и обучения нейронной сети могут быть использованы различные стандартные пакеты (например, TensorFlow или PyTorch), имеющие высокоуровневое API. Пример реализации архитектуры, аналогичной TadGAN, с использованием пакета TensorFlow для обучения весов можно посмотреть в репозитории [7]. При обучении этой модели оптимизировались пять метрик:
- aeLoss – среднеквадратичное отклонение между исходным и восстановленным временным рядом, т.е. разница между x и G(Ɛ(х)),
- cxLoss – бинарная кросс-энтропия критика Cx, определяющего разницу между истинным отрезком временного ряда и искусственно сгенерированным,
- cx_g_Loss – бинарная кросс-энтропия, ошибка генератора G(Ɛ(х)), характеризующая его неспособность «обманывать» критика Cx,
- czLoss - бинарная кросс-энтропия критика Cz, определяющего разницу между скрытым вектором, который сгенерировал кодировщик Ɛ и белым шумом, обеспечивает похожесть скрытого вектора Ɛ(х) на случайный вектор, не давая модели «заучивать» отдельные паттерны в исходных данных,
- cx_g_Loss – бинарная кросс-энтропия, ошибка генератора Ɛ(х), характеризующая его неспособность создавать скрытые векторы, похожие на случайные, и тем самым «обманывать» критика Cz.
После обучения модели проводится реконструкция отдельных отрезков исследуемого временного ряда и сравнение исходного и реконструированного ряда, которое может осуществляться одним из методов:
- поточечное сравнение;
- сравнение площадей кривых в заданной области вокруг каждого сэмпла (длина области - гиперпараметр);
- Dynamic Time Warping [9].
| Аномалия предсказана моделью, y_hat = 1 | Модель предсказала отсутствие аномалии | |
| Аномалия есть y = 1 | TP правильно предсказанная аномалия | FN аномалия есть, но ее не нашли |
| Аномалии нет y = 0 | FP предсказали аномалию там, где ее нет | TN аномалии нет и модель ее не видит |
График этого ряда:
Восстановленный ряд с использованием TadGAN для разного количества эпох (4 и 80) выглядит так:
Видно, что модель достаточно точно научилась предсказывать основные закономерности в данных. Попробуем добавить различные аномалии в данных и затем обнаружить их с помощью модели TadGAN. Сначала добавим несколько точечных аномалий.
Из графика исходного и предсказанного сигналов видно, что модель не может восстановить «пики» аномальных значений, что с высокой точностью может использоваться для определения точечных аномалий. Однако в такой ситуации польза сложной модели TadGAN неочевидна – подобные аномалии можно обнаружить и с помощью оценки превышения пороговых значений.
Теперь рассмотрим сигнал с другим типом аномалии - периодический сигнал с аномальным изменением частоты. В этом случае нет превышения порога – с точки зрения амплитуды все элементы ряда являются «нормальными» значениями, и аномалия выявляется только в групповом поведении нескольких точек. В этом случае TadGAN также не может восстановить сигнал (как это видно на рисунке) и это может быть использовано в качестве признака наличия групповой аномалии.
На этих двух примерах проиллюстрирована работа метода. Читатель и сам может попробовать создать свои датасеты и проверить возможности модели в различных ситуациях.
Более сложные примеры датасетов можно найти в статье авторов метода TadGAN [3]. Там же приведена ссылка на библиотеку Orion, являющуюся разработкой специалистов MIT, которая с использованием машинного обучения распознает редкие аномалии во временных рядах, используя подход обучения без учителя (unsupervised learning).
В заключении отметим, что методов, использующих реконструирование сигнала (reconstruction-based) для обнаружения аномалии сейчас очень много, например в ресурсе arxiv.org десятки статей, описывающих различные модификации подхода с использованием автокодировщиков и генеративных состязательных сетей. Для каждой конкретной задачи целесообразно подбирать свою модель, с учетом требований задачи и знаний о предметной области.
Поиск аномалий во временных рядах
Вокруг нас появляется все больше различных устройств, систем, комплексов, платформ – технологических, информационных, киберфизических. Мы не задумываемся о том, как кофеварка варит кофе, робот-пылесос...
habr.com