Для понимания этой статьи рекомендую ознакомиться с тем, что такое красно-черные деревья (КЧД) и тем, как они работают
При написании пар по алгоритмам и структурам данных, я столкнулся с тем, что существует достаточно мало материалов по AA-деревьям, а конкретных примеров и еще меньше. Так что это статья для таких же "ищущих" как и я
Для реализации будем использовать узел (ноду), что используется для реализации КЧД
from __future__ import annotations
from dataclasses import dataclass, field
from typing import Any, Literal
@dataclass
class Node:
key: Any
parent: Node | None = field(default=None)
right: Node | None = field(default=None)
left: Node | None = field(default=None)
height: int = field(default=1)
color: Literal["red", "black"] = field(default="black")
Высота здесь - это не количество нод от корня до узла, а отдельная величина для узла и увеличивается посредством операций при перебалансировке
Как определяется высота:
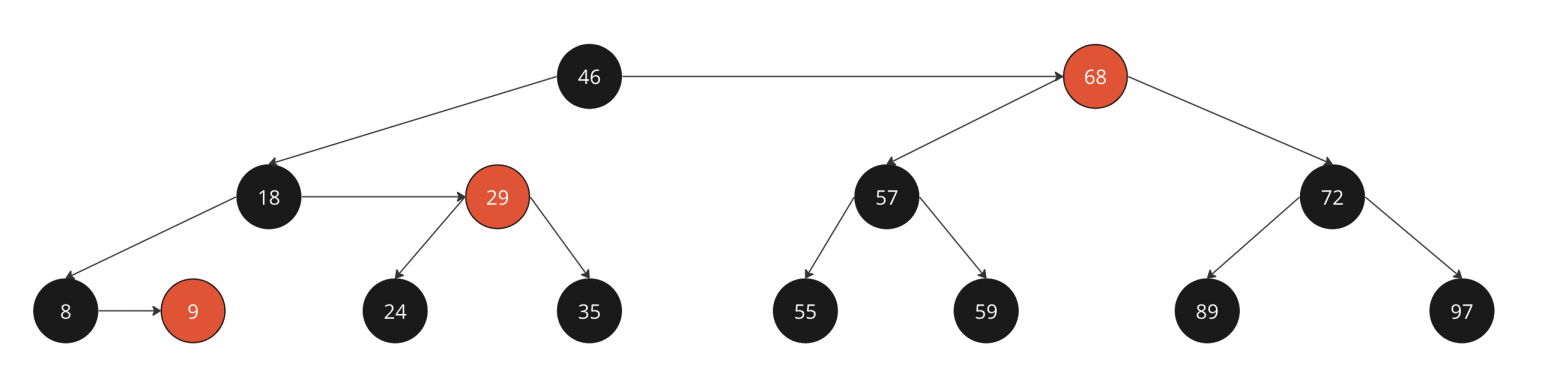
Пример AA-дерева
Корень - 46
Высота 1: 8, 9, 24, 35, ...
Высота 2: 18, 29, 57, 72
Высота 3: 46, 68
Связи м-ду нодами на одной высоте (46 и 68 например) называются горизонтальными
Горизонтальная связь всегда ведет к красной ноде

Левая горизонтальная свзяь
Обобщим такой случай

Обобщенная левая горизонтальная связь
X, Y, Z - некоторые поддеревья
Что делать в таком случае?
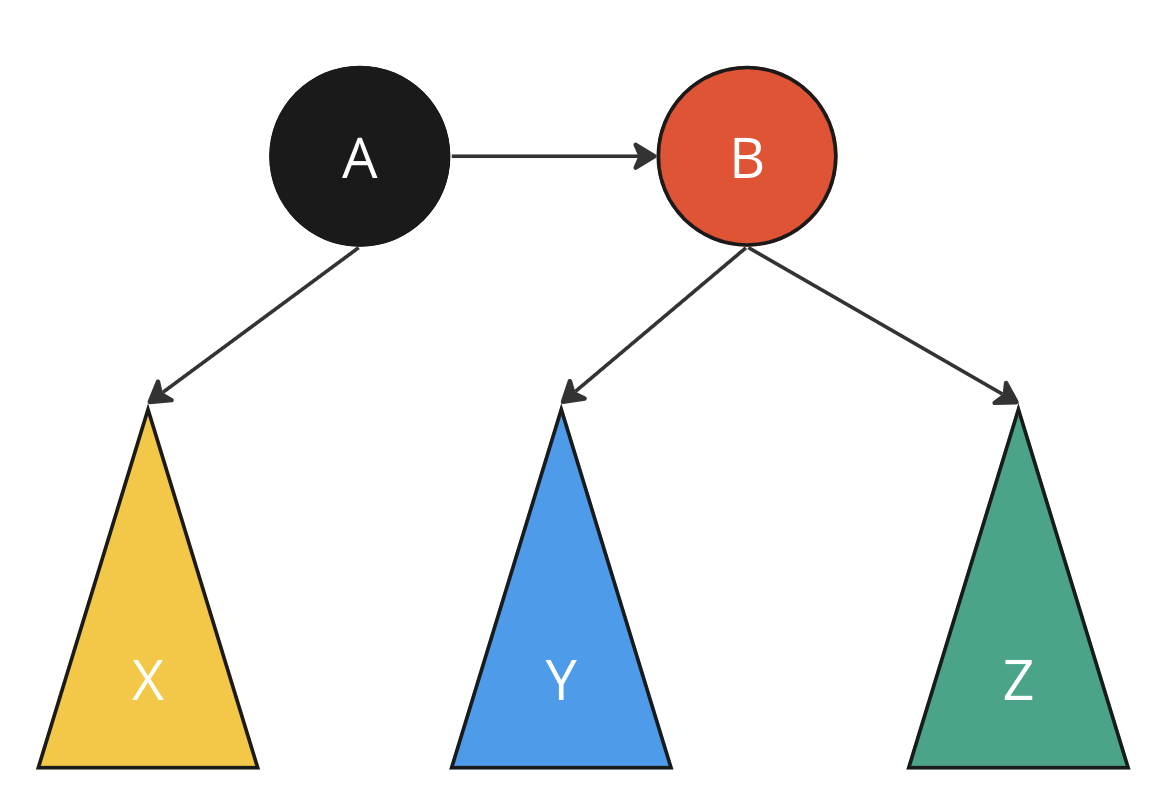
Убираем левую горизонтальную связь, операция skew
Назовем это преобразование skew
Благодаря тому, что последнее правило АА-дерево несиметрично (левого красного сына быть не может), симметричный кейс проблем у нас не вызывает
Применим skew к нашему примеру
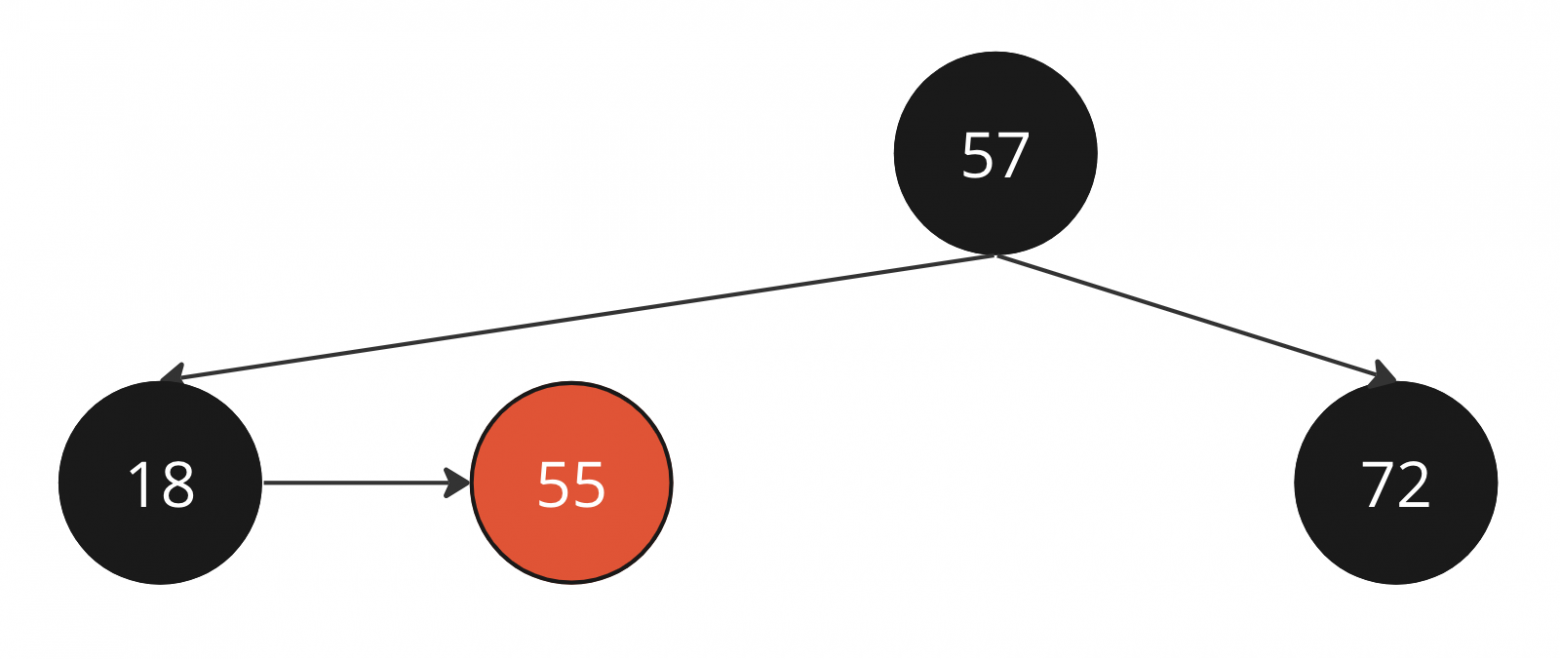
Применили skew, убрали левую горизонтальную связь
Реализуем skew
def skew(node: Node) -> Node:
child = node.left
subtree = child.right
node.left = subtree
subtree.parent = node
child.right = node
child.parent = node.parent
node.parent = child
child.color = "black"
node.color = "red"
return child
Теперь рассмотрим случай, если родитель красный
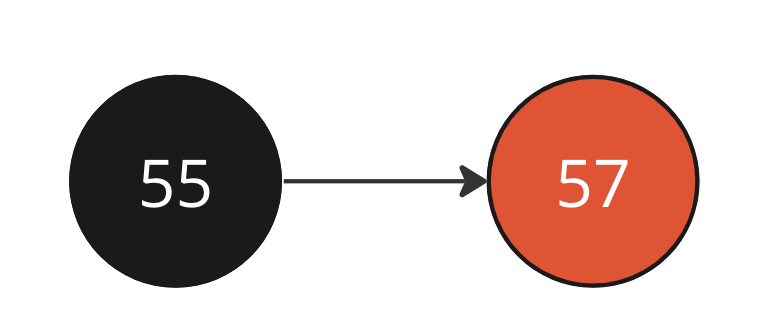
AA-дерево, добавим ноду 46
Добавляем в это дерево ноду 46 (слева от 55)
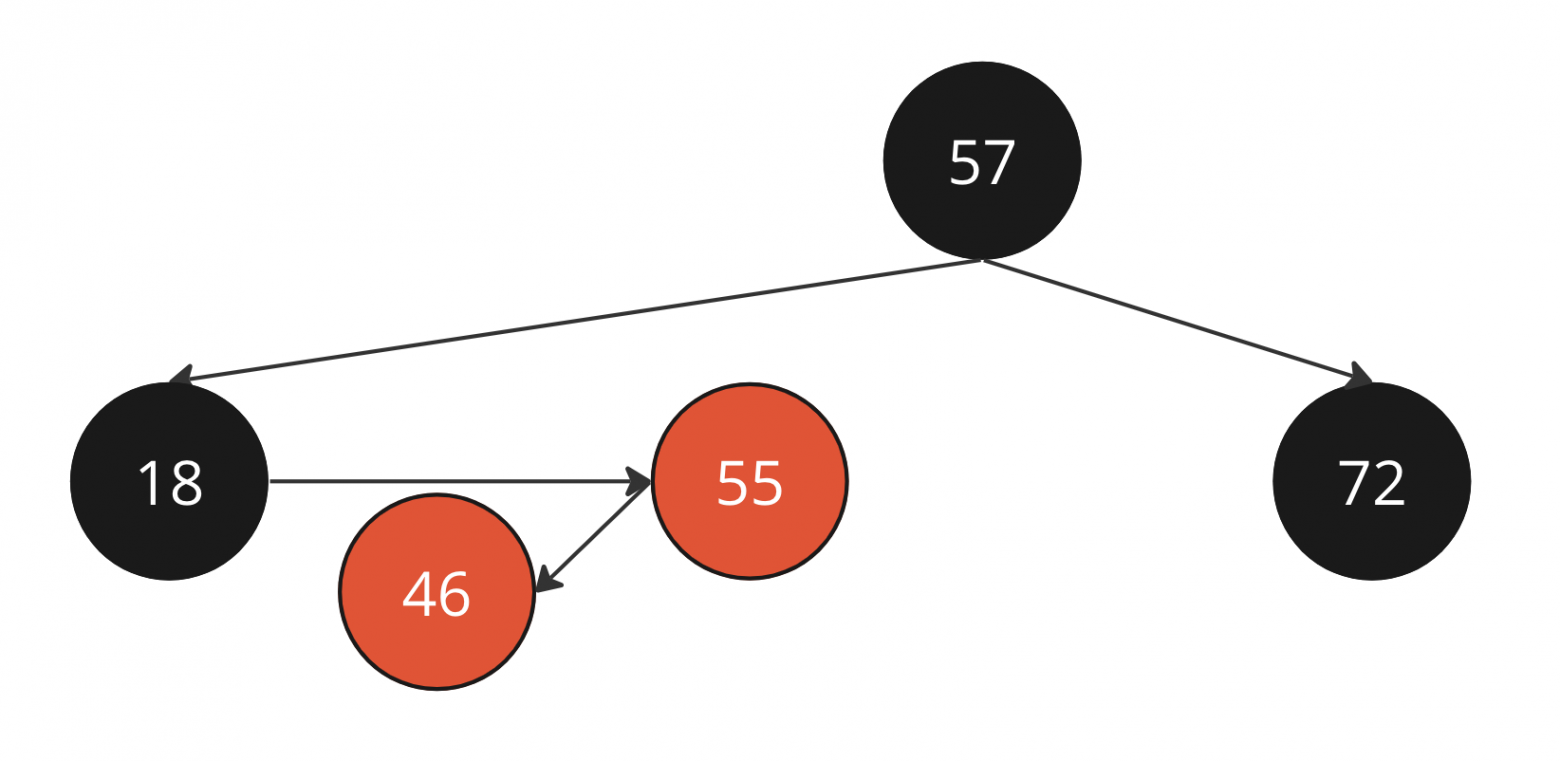
Нода 46 добавляется на одной высоте с 55
Получаем левую горизонтальную связь с красным родителем 55
Что делать?
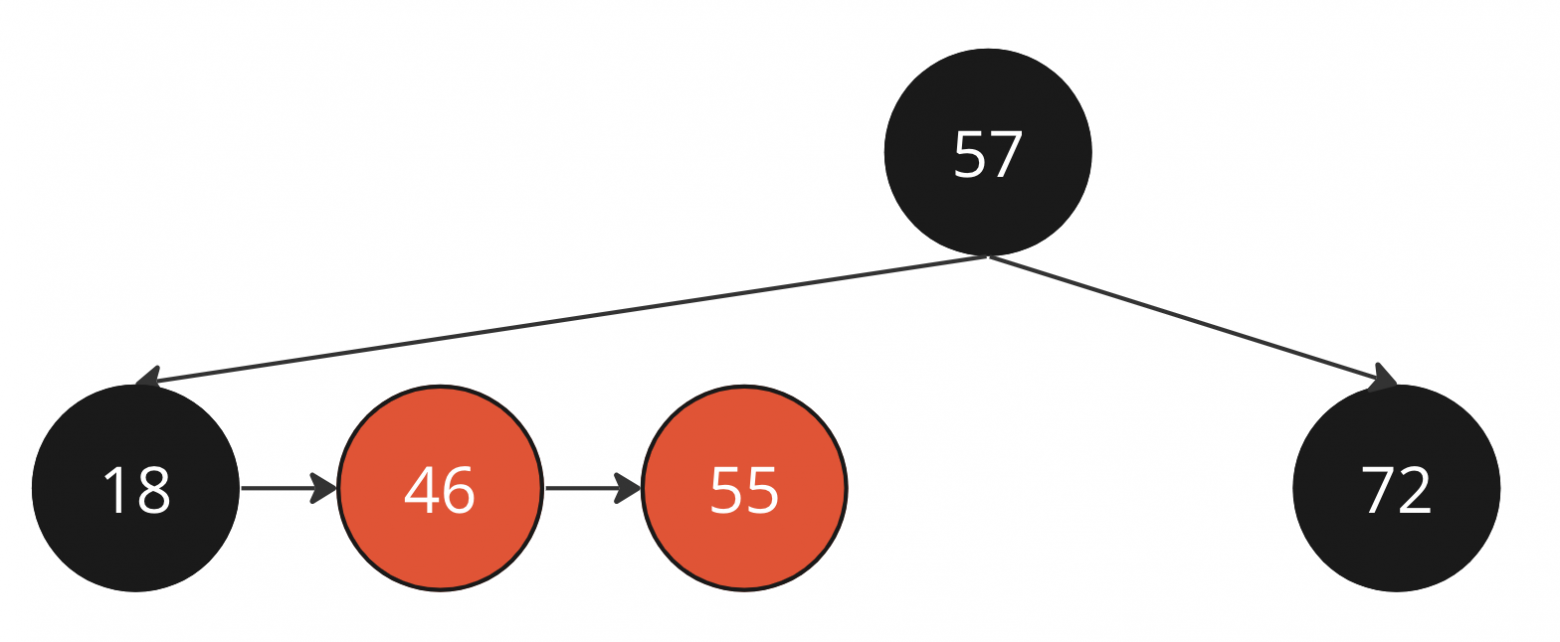
Убрали новую левую горизонтальную связь
Доработаем функцию skew
def skew(node: Node) -> Node:
child = node.left
subtree = child.right
node.left = subtree
subtree.parent = node
child.right = node
child.parent = node.parent
node.parent = child
if node.color == "black":
child.color = "black"
node.color = "red"
return child
Двойная левая горизонтальная связь невозможна, фиксится как 2 случая левой горизонтальной связи

Двойная горизонтальная связь
Обобщим этот случай

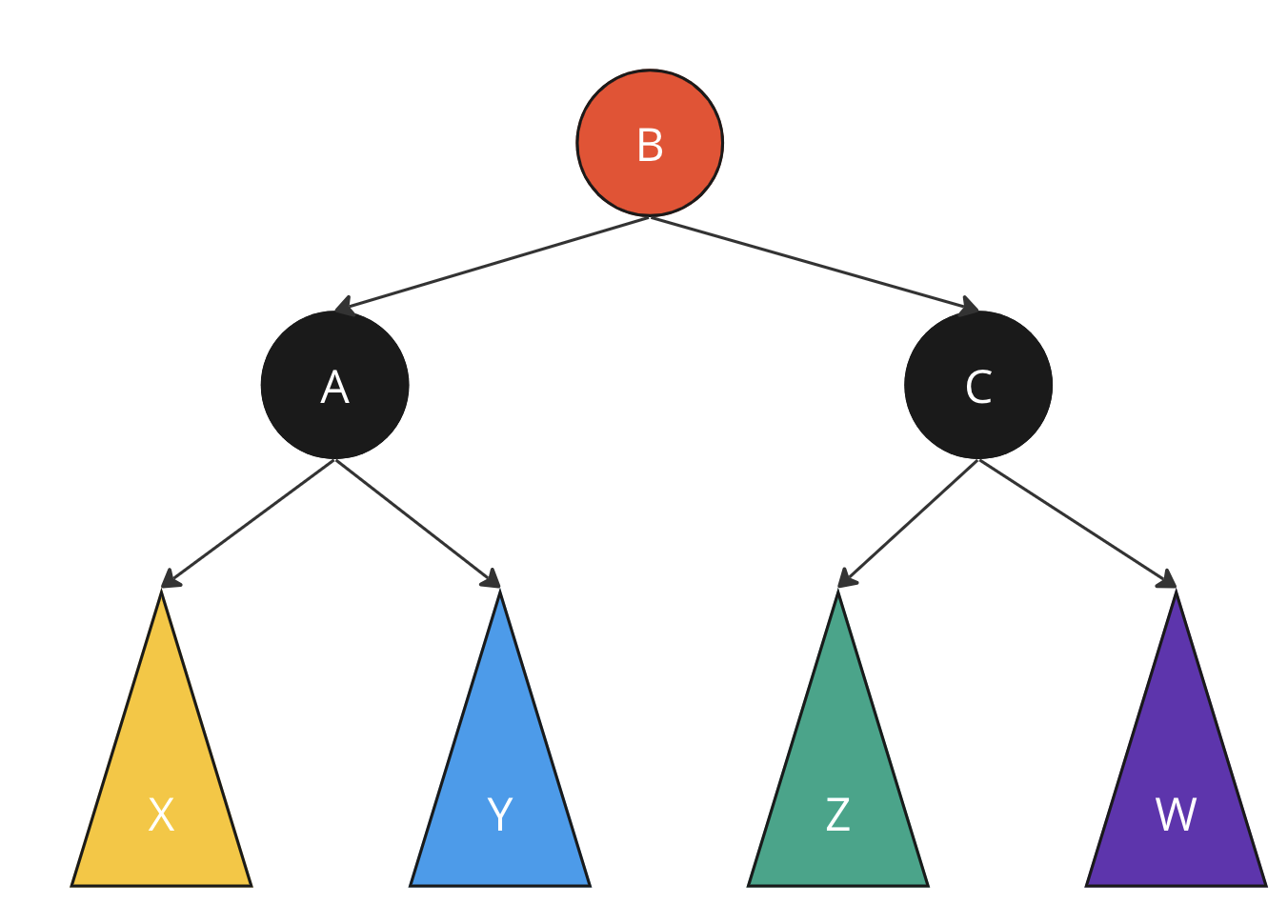
Обобщенный случай двойной горизонтальной связи
X, Y, Z, W - некоторые поддеревья
Что делаем?
Разрешение двойной горизонтальной связи
Назовем это преобразование split
По итогу преобразования можем получить 3 случая:
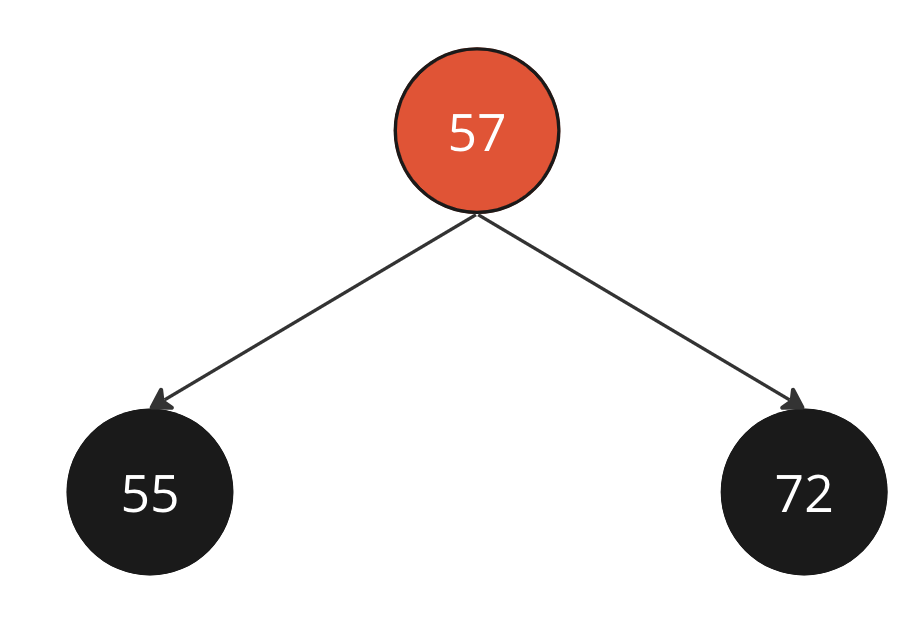
Разрешение двойной горизонтальной связи из примера
Реализуем split
def split(node: Node) -> Node:
child = node.right
subtree = child.left
child.parent = node.parent
node.parent = child
child.left = node
node.right = subtree
child.height += 1
child.right.color = "black"
return child
С полным процессом построения AA-дерева руками можно ознакомиться в видео ниже
Здесь строится дерево для массива [57, 55, 72, 18, 46, 68, 24, 9, 59, 97, 29, 35, 89, 8]
def insert_fix(tree: Node, node: Node):
while node.parent is not None:
if node.left is not None and node.left.color == "red":
node = skew(node)
elif node.right is not None and node.right.color == "red" and node.right.right is not None and node.right.right.color == "red":
node = split(node)
else:
node = node.parent
tree.color = "black"
А теперь сделаем непосредственно функцию вставки
def insert(tree: Node, key: Any):
parent = None
curr = tree
while curr is not None:
parent = curr
if key < curr.key:
curr = curr.left
else:
curr = curr.right
node = Node(key=key, color="red")
if parent is None:
tree = node
else:
node.parent = parent
node.height = parent.height
if key < parent.key:
parent.left = node
else:
parent.right = node
insert_fix(tree, node)
Будем рассматривать случаи на следующем дереве
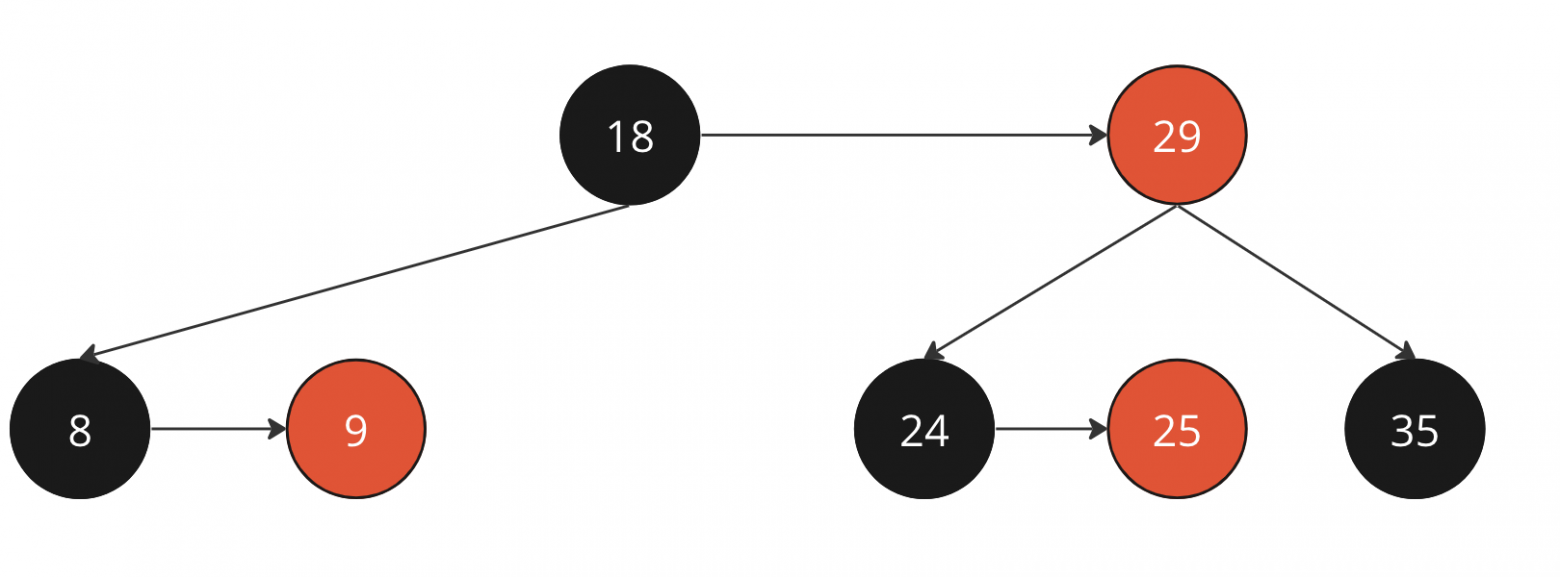
Пример дерева для удаления
В нашем примере - нода 9
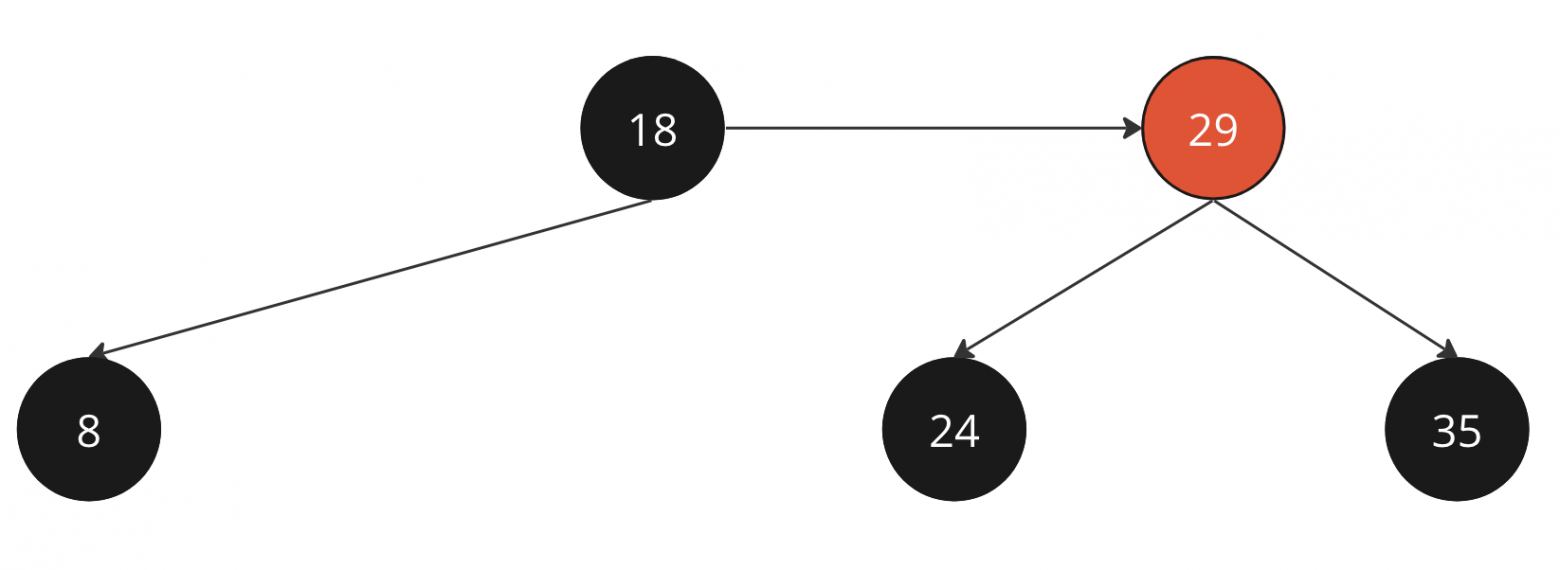
Дерево после удаления красного листа
Реализуем функцию удаления красного листа
def delete_red_leaf(node: Node):
parent = node.parent
parent.right = None
node.parent = None
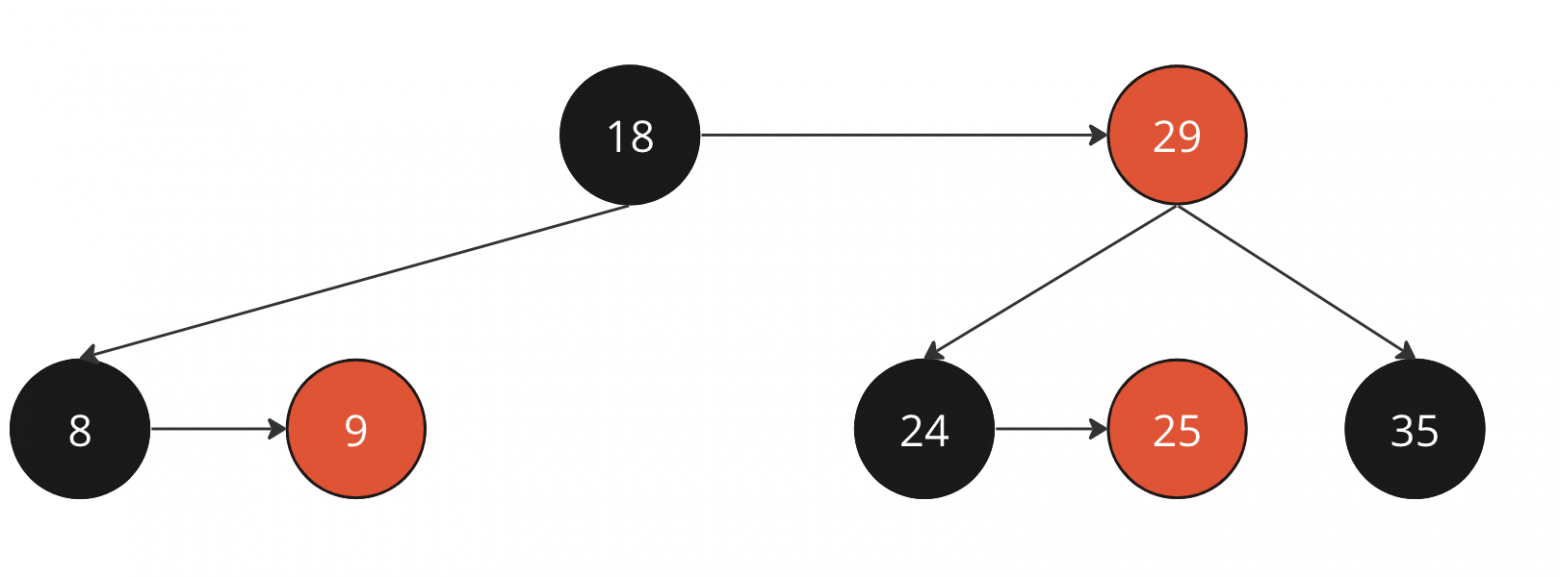
Пример дерева
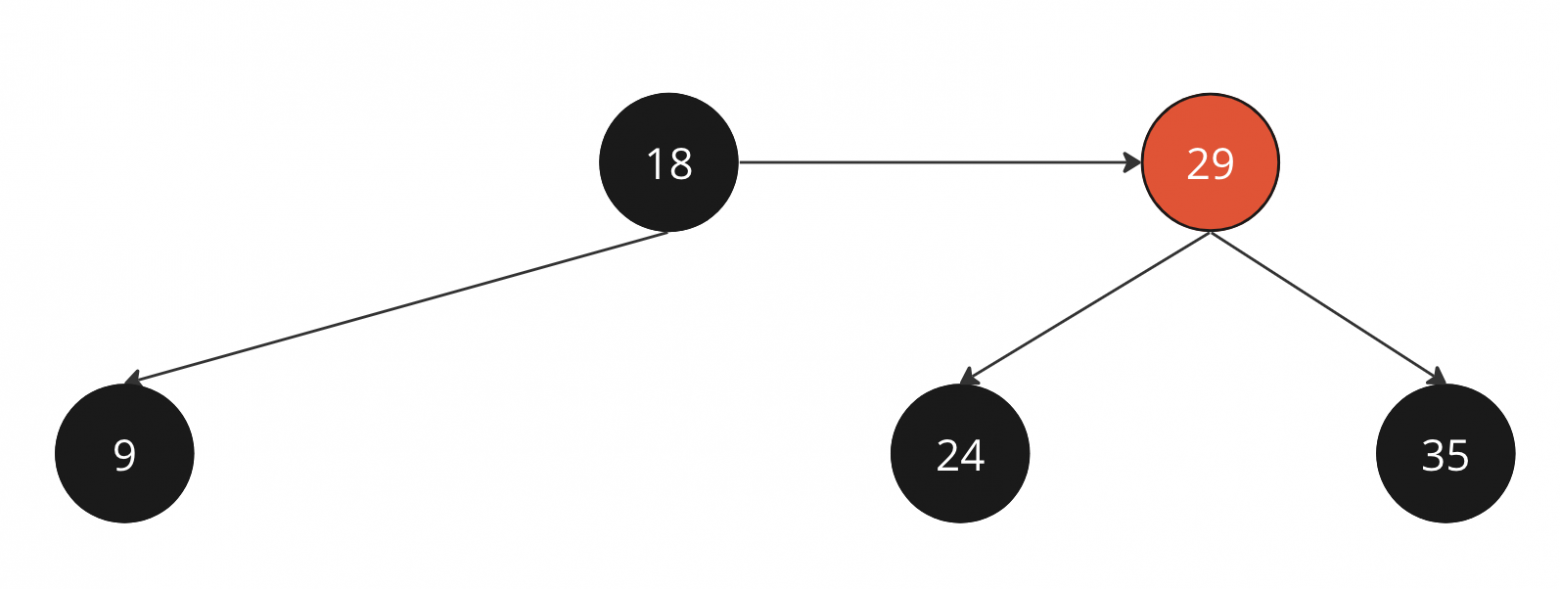
Дерево после удаления ноды 8
Реализуем функцию под этот случай
def remove_black_leaf_red_right(node: Node):
node.key = node.right.key
delete_red_leaf(node.right)
Назовем этот узел наследником
В зависимости от реализации наследниками могут быть:
Заменяем удаляемую ноду наследником и обрабатываем наследника:
def find_successor(node: Node):
successor = node.right
while successor.left is not None:
successor = successor.left
return successor

Пример дерева
Удалим ноду 18, наследник для нее - 24
Заменим значения и обработаем наследника по случаю 2
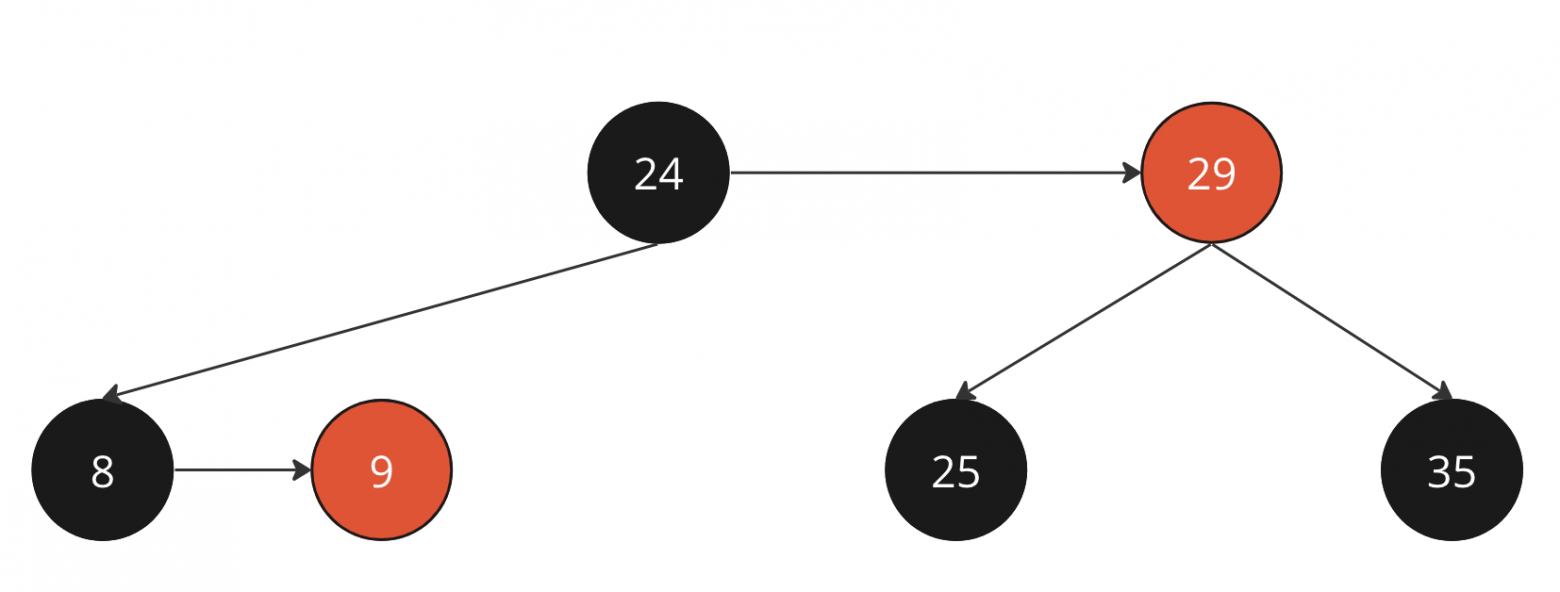
Удаляем 18 из дерева
Реализуем функцию
def delete_with_red_node_successor(node: Node)
successor = find_successor(node)
node.key = successor.key
remove_black_leaf_red_right(successor)
Для примера возьмем построенное выше дерево и попробуем удалить корень - 46
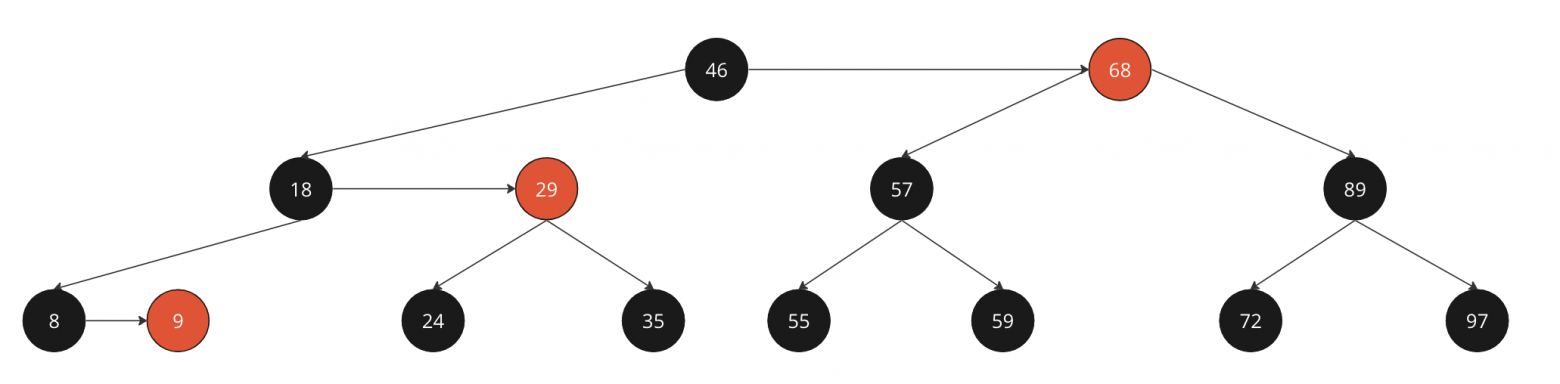
Построенное дерево из видео
Наследник корня - 55
Заменим значение и удалим наследника

Дерево после удаления ноды 55
У ноды 57 есть левый ребенок, который отличается по высоте от родителя на 2
(у None высота = 0, у ноды 57 высота = 2)
Уменьшаем высоту у ноды 57
Тк у 57 есть правый ребенок той же высоты (высоты 1), красим его в красный
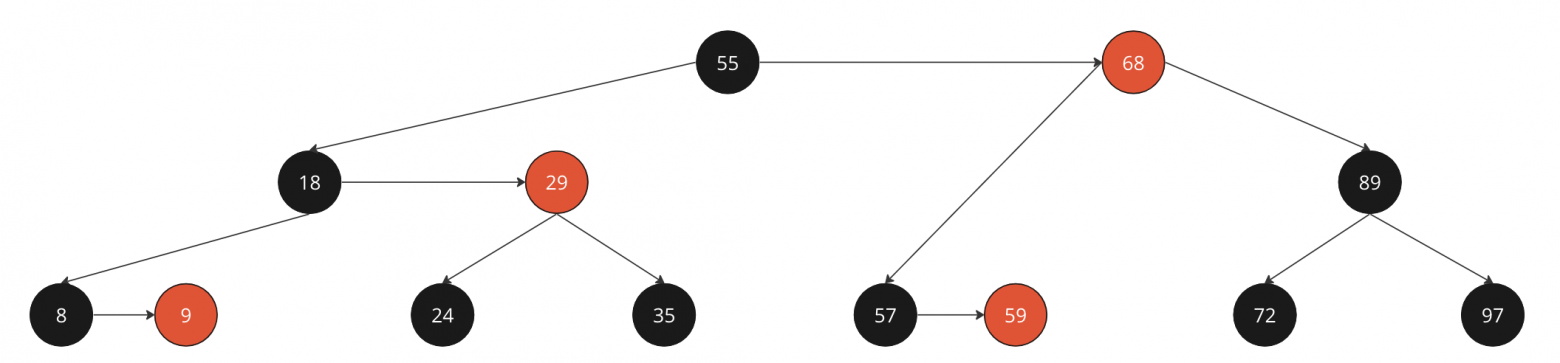
Уменьшаем высоту у ноды 57
Заметим, что у ноды 68 есть ребенок, отличающийся по высоте на 2 (нода 57)
Понизим высоту у ноды 68

Уменьшаем высоту 68
Покрасим ноды на одной высоте в красный
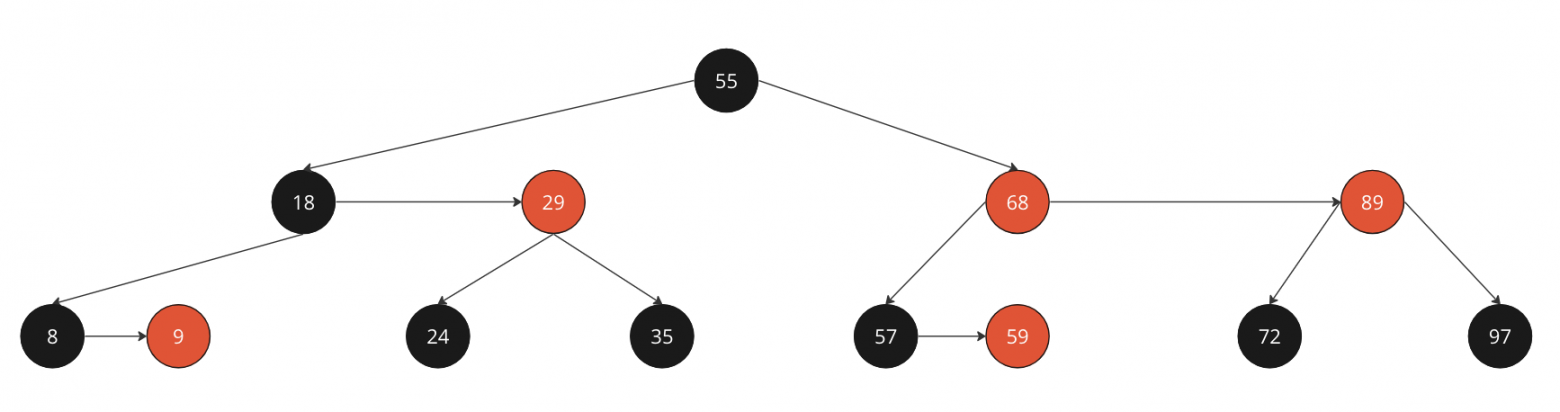
Нода 68 красная, у ноды 55 высота на 1 выше => красим 68 в черное
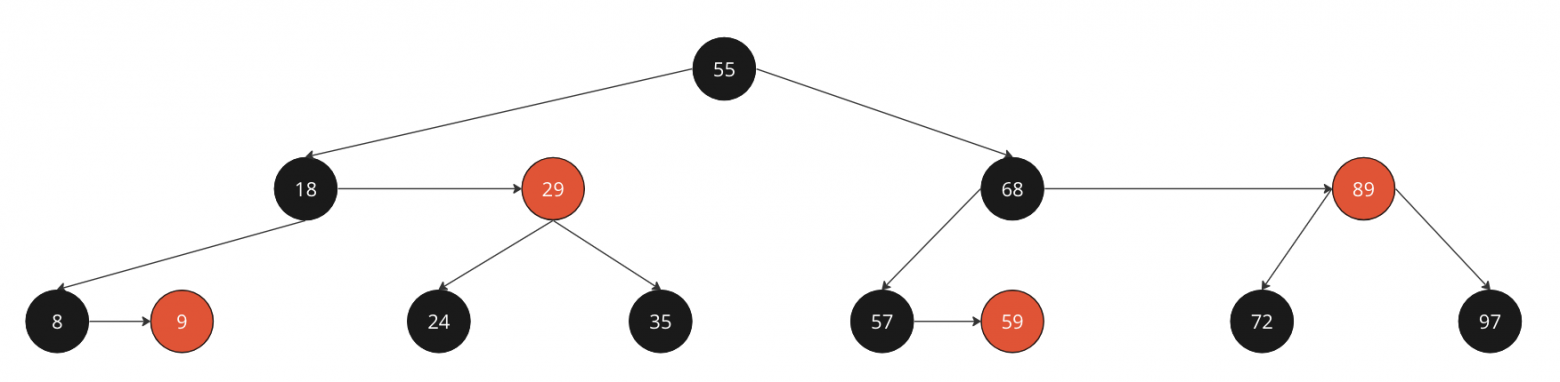
Перекрашиваем 68
Теперь попробуем удалить ноду 35, чтобы увидеть как работает skew при перебалансировке
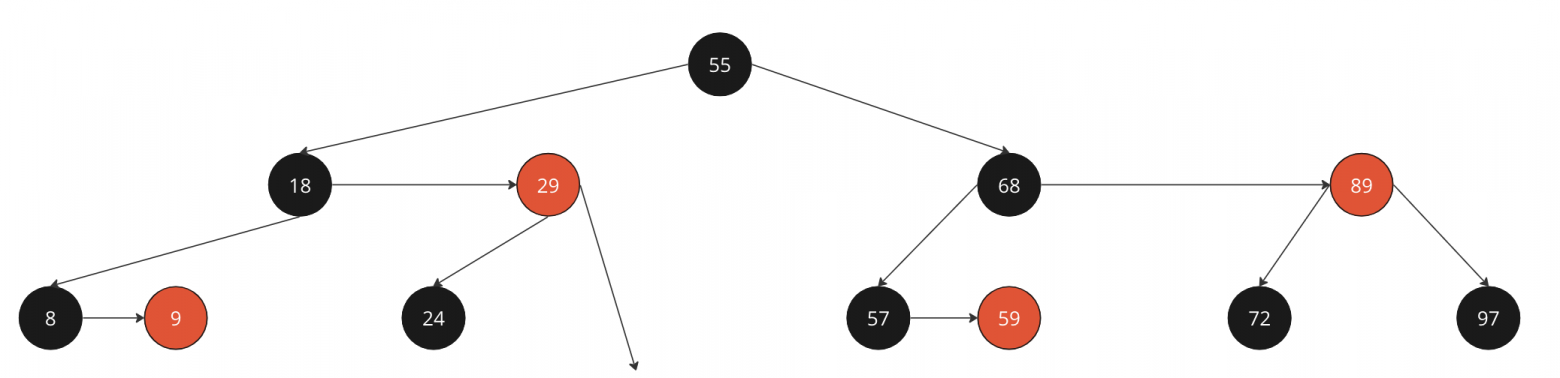
Удаляем 35
У 29 есть ребенок с высотой 0 => понижаем высоту 29 и красим 24 в красное

Дерево после понижения высоты
Делаем skew(29), напомню что в этом случае перекраска не происохдит
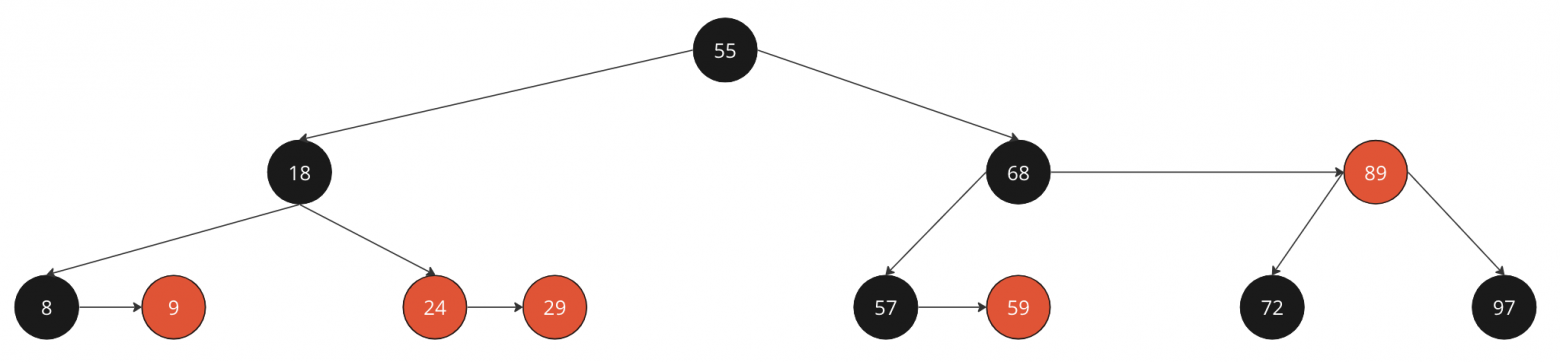
Произвели skew
Нода 24 красная, родитель - черный с высотой на 1 больше => красим 24 в черное
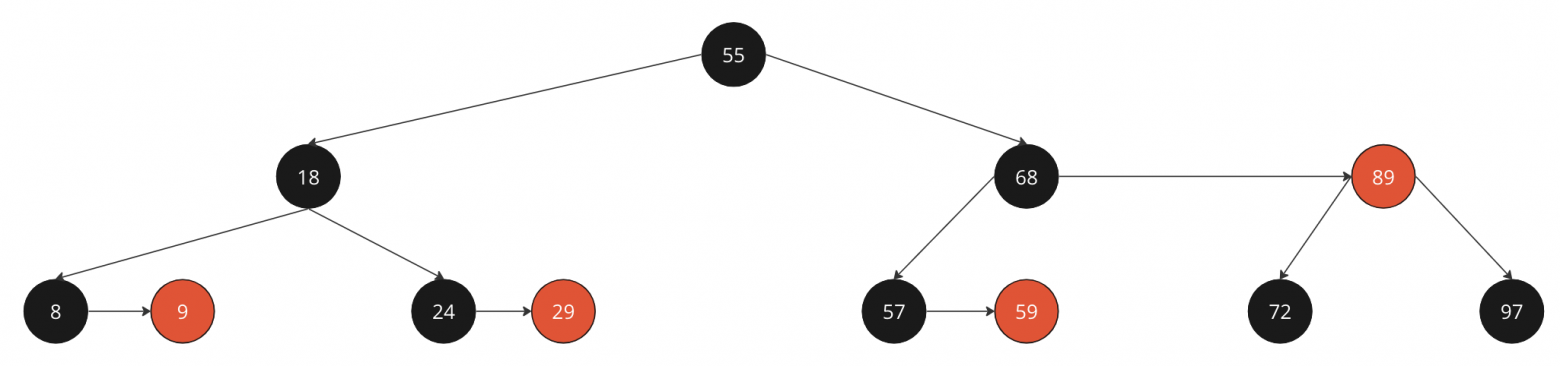
Перекрашиваем 24
Также есть визуализация алгоритма удаления, где используются и skew, и split, рекомендую ознакомиться
Реализуем функцию для этого случая
Для начала сделаем вспомогательные функции
def get_height(node: Node | None):
if node is None:
return 0
return node.height
def check_skew(node: Node):
return node.left.height == node.height and node.left.color == "left"
def check_split(node: Node):
child = node.right
grandson = child.right
return node.height == child.height and child.height == grandson.height and child.color == "red" and grandson.color == "red"
def decrease_height(node: Node):
node.height -= 1
if get_height(node.right) == node.height:
node.right = "red"
elif get_height(node.left) == node.height:
node.left = "red"
return node
А теперь непосредственно функция для рассмотренного случая
def delete_black_leaf(node: Node):
successor = find_successor(node)
node.key = successor.key
p = successor.parent
if p.left = successor:
p.left = None
else:
p.right = None
while p.parent is not None:
height = get_height(p)
if height - get_height(p.right) > 1 or height - get_height(p.left) > 1:
p = decrease_height(p)
if get_height(p.right) > node.height or p.right.color == "red":
decrease_height(node.right)
if p.left is not None and check_skew(p):
p = skew(p)
if p.right is not None and p.right.left is not None and check_skew(p.right):
p.right = skew(p.right)
if p.right is not None and p.right.right is not None and p.right.right.left is not None and check_skew(p.right.right):
p.right.right = skew(p.right.right)
if p.right is not None and p.right.right is not None check_split(p):
p = split(p)
if p.right is not None and p.right.right is not None and p.right.right.right is not None check_split(p.right):
p.right = split(p.right)
if p.color == "red" and p.parent.height > p.height:
p.color = "black"
p = p.parent
node = tree
if key < node.key:
node = node.left
elif key > node.key:
node = node.right
else:
if node.color == "red" and node.height == 1:
delete_red_leaf(node)
elif node.color == "black" and node.height == 1 and node.right is not None:
remove_black_leaf_red_right(node)
elif node.right is not None and node.left is not None:
successor = find_successor(node)
if successor.height == 1 and successor.right is not None:
delete_with_red_node_successor(node)
else:
delete_black_leaf(node)
else:
delete_black_leaf(node)

 habr.com
habr.com
При написании пар по алгоритмам и структурам данных, я столкнулся с тем, что существует достаточно мало материалов по AA-деревьям, а конкретных примеров и еще меньше. Так что это статья для таких же "ищущих" как и я
Что такое AA-дерево?
АА-дерево - это модификация красно-черного дерева с целью упрощения реализацииДля реализации будем использовать узел (ноду), что используется для реализации КЧД
from __future__ import annotations
from dataclasses import dataclass, field
from typing import Any, Literal
@dataclass
class Node:
key: Any
parent: Node | None = field(default=None)
right: Node | None = field(default=None)
left: Node | None = field(default=None)
height: int = field(default=1)
color: Literal["red", "black"] = field(default="black")
- key - полезная информация в ноде (строка, число, etc.)
- parent - ссылка на родительскую ноду
- right - ссылка на правого ребенка
- left - ссылка на левого ребенка
- height - высота
- color - цвет
- Цвет вершины может быть черным или красным
- Корень всегда черный
- Листья всегда черные
- Каждая красная вершина должна иметь двух черных сыновей
- Пути от вершины к ее листьям должны содержать одинаковое количество черных вершин (черная высота)
- В дереве не может быть левого красного сына
Высота здесь - это не количество нод от корня до узла, а отдельная величина для узла и увеличивается посредством операций при перебалансировке
Как определяется высота:
- У None листьев высота = 0
- У листьев высота = 1
- У красных нод высота та же, что и у его родителя
- У черных нод высота на 1 меньше, чем у их родителей

Пример AA-дерева
Корень - 46
Высота 1: 8, 9, 24, 35, ...
Высота 2: 18, 29, 57, 72
Высота 3: 46, 68
Связи м-ду нодами на одной высоте (46 и 68 например) называются горизонтальными
Горизонтальная связь всегда ведет к красной ноде
Вставка элемента в AA-дерево
Делается по аналогии с красно-черным деревом- Ищем куда добавить ноду
- Добавляем красную ноду
- Производим балансировку
Случай 1. Корень красный
По аналогии с КЧД, просто красим ноду в красныйСлучай 2. Левая горизонтальная связь
Для начала рассмотрим случай если родитель черный
Левая горизонтальная свзяь
Обобщим такой случай

Обобщенная левая горизонтальная связь
X, Y, Z - некоторые поддеревья
Что делать в таком случае?
- Правый поворот м-ду левым сыном (A) и отцом (B)
- Перекрашиваем сына в черное
- Перекрашиваем отца в красное

Убираем левую горизонтальную связь, операция skew
Назовем это преобразование skew
Благодаря тому, что последнее правило АА-дерево несиметрично (левого красного сына быть не может), симметричный кейс проблем у нас не вызывает
Применим skew к нашему примеру

Применили skew, убрали левую горизонтальную связь
Реализуем skew
def skew(node: Node) -> Node:
child = node.left
subtree = child.right
node.left = subtree
subtree.parent = node
child.right = node
child.parent = node.parent
node.parent = child
child.color = "black"
node.color = "red"
return child
Теперь рассмотрим случай, если родитель красный

AA-дерево, добавим ноду 46
Добавляем в это дерево ноду 46 (слева от 55)

Нода 46 добавляется на одной высоте с 55
Получаем левую горизонтальную связь с красным родителем 55
Что делать?
- Правый поворот м-ду сыном и отцом

Убрали новую левую горизонтальную связь
Доработаем функцию skew
def skew(node: Node) -> Node:
child = node.left
subtree = child.right
node.left = subtree
subtree.parent = node
child.right = node
child.parent = node.parent
node.parent = child
if node.color == "black":
child.color = "black"
node.color = "red"
return child
Случай 3. Двойная горизонтальная связь
Речь пойдет о двойной правой горизонтальной связиДвойная левая горизонтальная связь невозможна, фиксится как 2 случая левой горизонтальной связи

Двойная горизонтальная связь
Обобщим этот случай

Обобщенный случай двойной горизонтальной связи
X, Y, Z, W - некоторые поддеревья
Что делаем?
- Левый поворот м-ду A и B
- Увеличиваем высоту у B
- Перекрашиваем C в черный

Разрешение двойной горизонтальной связи
Назовем это преобразование split
По итогу преобразования можем получить 3 случая:
- B становится корнем дерева
- Обрабатываем как первый случай
- B образовывает левую горизонтальную связь
- Обрабатываем как второй случай
- B образовывает правую горизонтальную связь
- Тут проблем нет

Разрешение двойной горизонтальной связи из примера
Реализуем split
def split(node: Node) -> Node:
child = node.right
subtree = child.left
child.parent = node.parent
node.parent = child
child.left = node
node.right = subtree
child.height += 1
child.right.color = "black"
return child
С полным процессом построения AA-дерева руками можно ознакомиться в видео ниже
Здесь строится дерево для массива [57, 55, 72, 18, 46, 68, 24, 9, 59, 97, 29, 35, 89, 8]
Соберем весь код вставки
Сначала сделаем функцию которая будет исправлять все проблемы при перебалансировкеdef insert_fix(tree: Node, node: Node):
while node.parent is not None:
if node.left is not None and node.left.color == "red":
node = skew(node)
elif node.right is not None and node.right.color == "red" and node.right.right is not None and node.right.right.color == "red":
node = split(node)
else:
node = node.parent
tree.color = "black"
А теперь сделаем непосредственно функцию вставки
def insert(tree: Node, key: Any):
parent = None
curr = tree
while curr is not None:
parent = curr
if key < curr.key:
curr = curr.left
else:
curr = curr.right
node = Node(key=key, color="red")
if parent is None:
tree = node
else:
node.parent = parent
node.height = parent.height
if key < parent.key:
parent.left = node
else:
parent.right = node
insert_fix(tree, node)
Удаление элемента из AA-дерева
Рассмотрим 4 возможных случаяБудем рассматривать случаи на следующем дереве

Пример дерева для удаления
Случай 1. Удаляем красный лист
Просто удаляем лист, ничего больше не нужно т.к. черная высота не изменяетсяВ нашем примере - нода 9

Дерево после удаления красного листа
Реализуем функцию удаления красного листа
def delete_red_leaf(node: Node):
parent = node.parent
parent.right = None
node.parent = None
Случай 2. Удаляем черный лист с красной нодой
- Удаляем ребенка
- Заменяем значение ноды на значение ребенка
- Перекрашиваем ноду в черный

Пример дерева

Дерево после удаления ноды 8
Реализуем функцию под этот случай
def remove_black_leaf_red_right(node: Node):
node.key = node.right.key
delete_red_leaf(node.right)
Случай 3. Удаляем узел с двумя детьми
Для замены значения в удаляемой ноде нам необходимо найти некоторый узелНазовем этот узел наследником
В зависимости от реализации наследниками могут быть:
- Минимальное значение, большее чем текущее ("потомок")
- Максимальное значение, меньшее чем текущее ("предшественник")
Заменяем удаляемую ноду наследником и обрабатываем наследника:
- Если наследник - черный лист с красной нодой, обрабатываем как второй случай
- Иначе - см. случай 4 (см. ниже)
def find_successor(node: Node):
successor = node.right
while successor.left is not None:
successor = successor.left
return successor

Пример дерева
Удалим ноду 18, наследник для нее - 24
Заменим значения и обработаем наследника по случаю 2

Удаляем 18 из дерева
Реализуем функцию
def delete_with_red_node_successor(node: Node)
successor = find_successor(node)
node.key = successor.key
remove_black_leaf_red_right(successor)
Случай 4. Удаляем черный лист
Самый сложный случай- Удаляем ноду
- Идем от удаленной ноды до корня
- Для каждой ноды (𝑝) на пути с двумя детьми делаем следующее:
- Если есть ребенок с высотой с разницей в 2 по сравнению с текущим:
- Уменьшаем высоту 𝑝
- Если правый ребенок - красный, уменьшаем и его высоту
- При необходимости делаем
- skew(𝑝)
- skew(𝑝.𝑟𝑖𝑔ℎ𝑡)
- skew(𝑝.𝑟𝑖𝑔ℎ𝑡.𝑟𝑖𝑔ℎ𝑡)
- split(𝑝)
- split(𝑝.𝑟𝑖𝑔ℎ𝑡)
- Если 𝑝 - красный и у родителя высота больше, красим 𝑝 в черный
- Если есть ребенок с высотой с разницей в 2 по сравнению с текущим:
Для примера возьмем построенное выше дерево и попробуем удалить корень - 46

Построенное дерево из видео
Наследник корня - 55
Заменим значение и удалим наследника

Дерево после удаления ноды 55
У ноды 57 есть левый ребенок, который отличается по высоте от родителя на 2
(у None высота = 0, у ноды 57 высота = 2)
Уменьшаем высоту у ноды 57
Тк у 57 есть правый ребенок той же высоты (высоты 1), красим его в красный

Уменьшаем высоту у ноды 57
Заметим, что у ноды 68 есть ребенок, отличающийся по высоте на 2 (нода 57)
Понизим высоту у ноды 68

Уменьшаем высоту 68
Покрасим ноды на одной высоте в красный

Нода 68 красная, у ноды 55 высота на 1 выше => красим 68 в черное

Перекрашиваем 68
Теперь попробуем удалить ноду 35, чтобы увидеть как работает skew при перебалансировке

Удаляем 35
У 29 есть ребенок с высотой 0 => понижаем высоту 29 и красим 24 в красное

Дерево после понижения высоты
Делаем skew(29), напомню что в этом случае перекраска не происохдит

Произвели skew
Нода 24 красная, родитель - черный с высотой на 1 больше => красим 24 в черное

Перекрашиваем 24
Также есть визуализация алгоритма удаления, где используются и skew, и split, рекомендую ознакомиться
Реализуем функцию для этого случая
Для начала сделаем вспомогательные функции
def get_height(node: Node | None):
if node is None:
return 0
return node.height
def check_skew(node: Node):
return node.left.height == node.height and node.left.color == "left"
def check_split(node: Node):
child = node.right
grandson = child.right
return node.height == child.height and child.height == grandson.height and child.color == "red" and grandson.color == "red"
def decrease_height(node: Node):
node.height -= 1
if get_height(node.right) == node.height:
node.right = "red"
elif get_height(node.left) == node.height:
node.left = "red"
return node
А теперь непосредственно функция для рассмотренного случая
def delete_black_leaf(node: Node):
successor = find_successor(node)
node.key = successor.key
p = successor.parent
if p.left = successor:
p.left = None
else:
p.right = None
while p.parent is not None:
height = get_height(p)
if height - get_height(p.right) > 1 or height - get_height(p.left) > 1:
p = decrease_height(p)
if get_height(p.right) > node.height or p.right.color == "red":
decrease_height(node.right)
if p.left is not None and check_skew(p):
p = skew(p)
if p.right is not None and p.right.left is not None and check_skew(p.right):
p.right = skew(p.right)
if p.right is not None and p.right.right is not None and p.right.right.left is not None and check_skew(p.right.right):
p.right.right = skew(p.right.right)
if p.right is not None and p.right.right is not None check_split(p):
p = split(p)
if p.right is not None and p.right.right is not None and p.right.right.right is not None check_split(p.right):
p.right = split(p.right)
if p.color == "red" and p.parent.height > p.height:
p.color = "black"
p = p.parent
Соберем весь код удаления
def delete(tree: Node, key: Any):node = tree
if key < node.key:
node = node.left
elif key > node.key:
node = node.right
else:
if node.color == "red" and node.height == 1:
delete_red_leaf(node)
elif node.color == "black" and node.height == 1 and node.right is not None:
remove_black_leaf_red_right(node)
elif node.right is not None and node.left is not None:
successor = find_successor(node)
if successor.height == 1 and successor.right is not None:
delete_with_red_node_successor(node)
else:
delete_black_leaf(node)
else:
delete_black_leaf(node)
Разбираемся в АА-деревьях (Python)
Для понимания этой статьи рекомендую ознакомиться с тем, что такое красно-черные деревья (КЧД) и тем, как они работают При написании пар по алгоритмам и структурам данных, я столкнулся с тем, что...
