Аппарат линейной алгебры применяют в самых разных областях — в линейном программировании, эконометрике, в естественных науках. Отдельно отмечу, что этот раздел математики востребован в машинном обучении. Если, например, вам нужно поработать с матрицами и векторами, то, вполне возможно, на каком-то шаге вам придётся решать систему линейных алгебраических уравнений (СЛАУ).
СЛАУ — мощный инструмент моделирования процессов. Если некая хорошо изученная модель на основе СЛАУ годится для формализации задачи, то с высокой вероятностью её можно будет решить. А вот насколько быстро — это зависит от вашего инструментария и вычислительных мощностей.
Я расскажу про один из таких инструментов — Python-пакет scipy.linalg из библиотеки SciPy, который позволяет быстро и эффективно решать многие задачи с использованием аппарата линейной алгебры.
В этом туториале вы узнаете:
Если можно — сделай тут habraCUT! Важно, чтобы этот ^^ список люди прочитали и заинтересовались
Когда речь идёт о математике, изложение материала должно быть последовательным — таким, чтобы одно следовало из другого. Эта статья не исключение: сначала будет много подготовительной информации и только потом мы перейдём непосредственно к делу.
Если готовы к этому — приглашаю под кат. Хотя, честно говоря, некоторые разделы можно пропускать — например, основы работы с векторами и матрицами в NumPy (если вы хорошо знакомы с ним).
SciPy — это библиотека Python с открытым исходным кодом для научных вычислений: решение СЛАУ, оптимизация, интеграция, интерполяция и обработка сигналов. Помимо linalg, она содержит несколько других пакетов — например, NumPy, Matplotlib, SymPy, IPython и pandas.
Среди прочего, scipy.linalg содержит функции для с работы с матрицами — вычисление определителя, инверсия, вычисление собственных значений и векторов, а также сингулярное разложение.
Чтобы использовать scipy.linalg, вам необходимо установить и настроить библиотеку SciPy. Это можно сделать с помощью дистрибутива Anaconda, а также системы управления пакетами и инсталлятора Conda.
Для начала подготовьте среду выполнения для библиотеки:
$ conda create --name linalg
$ conda activate linalg
Установите необходимые пакеты:
(linalg) $ conda install scipy jupyter
Эта команда может работать долго. Не пугайтесь!
Я предлагаю использовать Jupyter Notebook для запуска кода в интерактивной среде. Это не обязательно, но лично мне он облегчает работу.
Перед открытием Jupyter Notebook вам необходимо зарегистрировать экземпляр conda linalg, чтобы использовать его в качестве ядра при создании ноутбука. Для этого выполните следующую команду:
(linalg) $ python -m ipykernel install --user --name linalg
Теперь можно открыть Jupyter Notebook:
$ jupyter notebook
Когда он загрузится в вашем браузере, создайте новый notebook, нажав New → linalg:
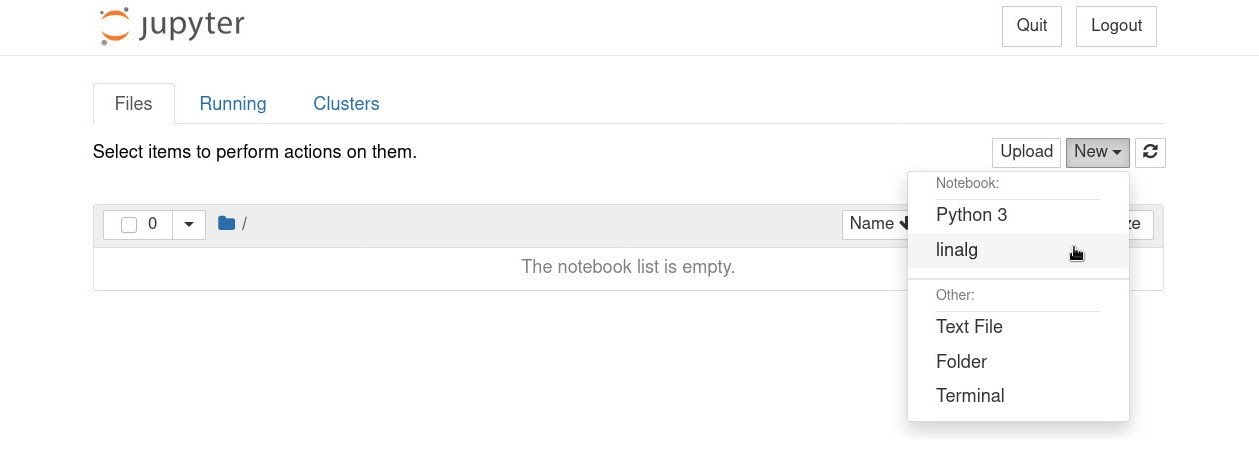
Чтобы убедиться, что установка библиотеки SciPy прошла успешно, введите в ноутбуке:
>>>
In [1]: import scipy
Сложно переоценить роль векторов и матриц при решении технических задач и, в том числе, задач машинного обучения.
NumPy — это наиболее популярный пакет для работы с матрицами и векторами в Python. Часто его применяют в сочетании с scipy.linalg. Чтобы начать работу с матрицами и векторами, нужно импортировать пакет NumPy:
>>>
In [2]: import numpy as np
Для представления матриц и векторов NumPy использует специальный тип, называемый ndarray. Чтобы создать объект ndarray, вы можете использовать array ().
Например, вам нужно создать следующую матрицу:
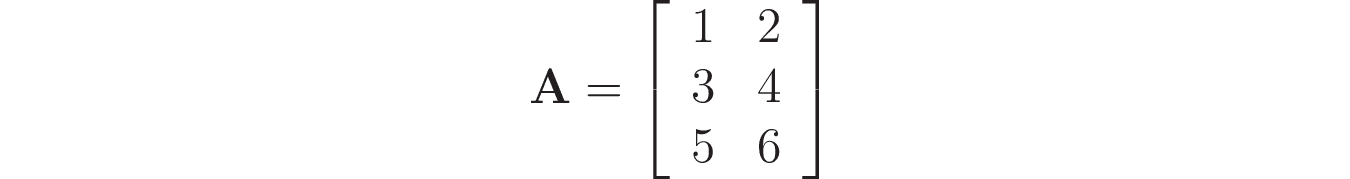
Создадим матрицу как набор вложенных списков (векторов-строк):
>>>
In [3]: A = np.array([[1, 2], [3, 4], [5, 6]])
...: A
Out[3]:
array([[1, 2],
[3, 4],
[5, 6]])
Заметьте, что приведённый выше вывод (Outp[3]) достаточно наглядно показывает получившуюся матрицу.
И ещё: все элементы матрицы должны и будут иметь один тип. Это можно проверить с помощью dtype.
>>>
In [4]: A.dtype
Out[4]:
dtype('int64')
Здесь элементы являются целыми числами, поэтому их общий тип по умолчанию — int64. Если бы среди них было хотя бы одно число с плавающей точкой, все элементы получили бы тип float64:
>>>
In [5]: A = np.array([[1.0, 2], [3, 4], [5, 6]])
...: A
Out[5]:
array([[1., 2.],
[3., 4.],
[5., 6.]])
In [6]: A.dtype
Out[6]:
dtype('float64')
Чтобы вывести на экран размерность матрицы, можно использовать метод shape:
>>>
In [7]: A.shape
Out[7]:
(3, 2)
Как и ожидалось, размерность матрицы A 3×2, то есть A имеет три строки и два столбца.
При работе с матрицами часто приходится использовать операцию транспонирования, которая столбцы превращает в строки и наоборот. Чтобы транспонировать вектор или матрицу (представленную объектом типа ndarray), вы можете использовать .transpose () или .T. Например:
>>>
In [8]: A.T
Out[8]:
array([[1., 3., 5.],
[2., 4., 6.]])
Чтобы создать вектор, также можно использовать.array(), передав туда список значений в качестве аргумента:
>>>
In [9]: v = np.array([1, 2, 3])
...: v
Out[9]:
array([1, 2, 3])
По аналогии с матрицами, используем .shape(), чтобы вывести на экран размерность вектора:
>>>
In [10]: v.shape
Out[10]:
(3,)
Заметьте, что она выглядит как (3,), а не как (3, 1) или (1, 3). Разработчики NumPy решили сделать отображение размерности векторов так же, как в MATLAB.
Чтобы получить на выходе размерность (1, 3), нужно было бы создать вот такой массив:
>>>
In [11]: v = np.array([[1, 2, 3]])
...: v.shape
Out[11]:
(1, 3)
Для (3, 1) — вот такой:
>>>
In [12]: v = np.array([[1], [2], [3]])
...: v.shape
Out[12]:
(3, 1)
Как видите, они не идентичны.
Часто возникает задача из вектора-строки сделать вектор-столбец. Как вариант, можно сначала создать вектор-строку, а потом использовать .reshape() для его преобразования в столбец:
>>>
In [13]: v = np.array([1, 2, 3]).reshape(3, 1)
...: v.shape
Out[13]:
(3, 1)
В приведённом выше примере мы использовали .reshape() для получения вектора-столбца с размерностью (3, 1) из вектора с размерностью(3,). Стоит отметить, что .reshape() делает преобразование с учётом того, что количество элементов (100% заполненных мест) в массиве с новой размерностью должно быть равно количеству элементов в исходном массиве.
В практических задачах часто требуется создавать матрицы, полностью состоящие из нулей, единиц или случайных чисел. Для этого NumPy предлагает несколько удобных функций, о которых я расскажу в следующем разделе.
NumPy позволяет быстро создавать и заполнять массивы. Например, чтобы создать массив, заполненный нулями, можно использовать .zeros():
>>>
In [15]: A = np.zeros((3, 2))
...: A
Out[15]:
array([[0., 0.],
[0., 0.],
[0., 0.]])
В качестве аргумента .zeros() нужно указать размерность массива, упакованную в кортеж (перечислить значения через запятую и обернуть это в круглые скобки). Элементы созданного массива получат тип float64.
Точно так же, для создания массивов из единиц можно использовать .ones ():
>>>
In [16]: A = np.ones((2, 3))
...: A
Out[16]:
array([[1., 1., 1.],
[1., 1., 1.]])
Элементы созданного массива также получат тип float64.
Создать массив, заполненный случайными числами, поможет .random.rand():
>>>
In [17]: A = np.random.rand(3, 2)
...: A
Out[17]:
array([[0.8206045 , 0.54470809],
[0.9490381 , 0.05677859],
[0.71148476, 0.4709059 ]])
Говоря точнее, метод .random.rand() возвращает массив с псевдослучайными значениями (от 0 до 1) из множества, сгенерированного по закону равномерного распределения. Обратите внимание, что в отличие от .zeros() и .ones(), .random.rand () на вход принимает не кортеж, а просто два значения через запятую.
Чтобы получить массив с псевдослучайными значениями, взятыми из множества, сгенерированного по закону нормального распределения с нулевым средним и единичной дисперсией, вы можете использовать .random.randn():
>>>
In [18]: A = np.random.randn(3, 2)
...: A
Out[18]:
array([[-1.20019512, -1.78337814],
[-0.22135221, -0.38805899],
[ 0.17620202, -2.05176764]])
NumPy имеет встроенный модуль numpy.linalg для решения некоторых задач, связанных с аппаратом линейной алгебры. Обычно scipy.linalg рекомендуют использовать по следующим причинам:
Несмотря на то, что SciPy добавит зависимости в ваш проект, по возможности, используйте scipy.linalg вместо numpy.linalg.
В следующем разделе мы применим scipy.linalg для работы с системами линейных алгебраических уравнений. Наконец-то практика!
Пакет scipy.linalg может стать полезным инструментом для решения транспортной задачи, балансировки химических уравнений и электрических нагрузок, полиномиальной интерполяции и так далее.
В этом разделе вы узнаете, как использовать scipy.linalg.solve() для решения СЛАУ. Но прежде чем приступить к работе с кодом, займёмся формализацией задачи и далее рассмотрим простой пример.
Система линейных алгебраических уравнений — это набор из m уравнений, n переменных и вектора свободных членов. Прилагательное «линейных» означает, что все переменные имеют первую степень. Для простоты рассмотрим СЛАУ, где m и n равны 3:
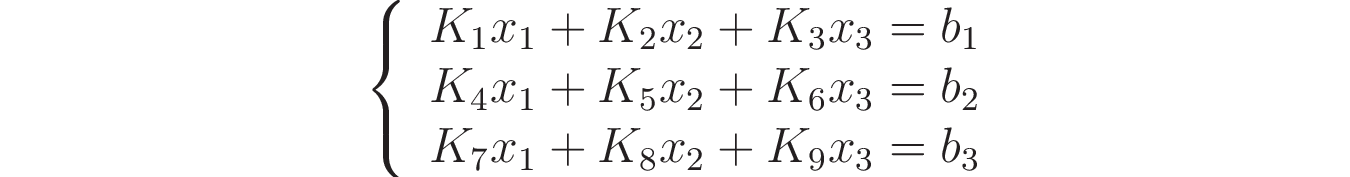
Есть ещё одно требование к «линейности»: коэффициенты K₁ … K₉ и вектор b₁ … b₃ должны быть константами (в математическом смысле этого слова).
В реальных задачах СЛАУ обычно содержат большое количество переменных, что делает невозможным решение систем вручную. К счастью, такие инструменты, как scipy.linalg, могут выполнить эту тяжелую работу.
Мы сначала разберёмся с основами scipy.linalg.solve() на простом примере, а в следующем разделе возьмём задачу посложнее.
Итак:
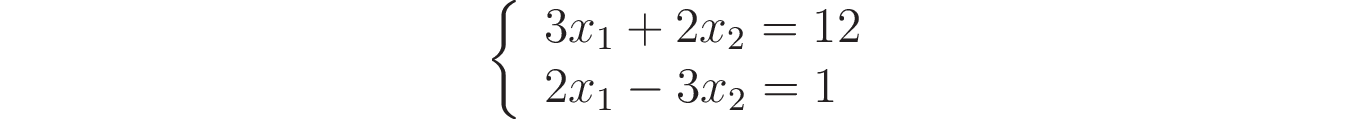
Перейдём к матричной записи нашей системы и введём соответствующие обозначения — A, x и b:

Заметьте: левая часть в исходной записи системы — это обычное произведение матрицы A на вектор x.
Всё, теперь можно переходить к программированию.
Входными данными для scipy.linalg.solve() будут матрица A и вектор b. Их нужно представить в виде двух массивов: A — массив 2х2 и b — массив 2х1. В этом нам как раз поможет NumPy. Таким образом, мы можем решить систему так:
>>>
1In [1]: import numpy as np
2 ...: from scipy.linalg import solve
3
4In [2]: A = np.array(
5 ...: [
6 ...: [3, 2],
7 ...: [2, -1],
8 ...: ]
9 ...: )
10
11In [3]: b = np.array([12, 1]).reshape((2, 1))
12
13In [4]: x = solve(A, b)
14 ...: x
15 Out[4]:
16 array([[2.],
17 [3.]])
Разберём приведённый выше код:
Если вы подставите x1 = 2 и x2 = 3 в исходные уравнения, будет ясно, что это действительно решение нашей системы.
Далее возьмём более сложный пример из реальной практики.
Это одна из типовых задач, встречающихся на практике: найти пропорции компонентов для получения определенной смеси.
Ниже мы сформируем план питания, смешивая разные продукты, чтобы получить сбалансированную диету.
Нам даны нормы содержания витаминов в пище:
В следующей таблице представлены результаты анализа продуктов. В одном грамме каждого продукта содержится некоторое количество витаминов:
Необходимо скомбинировать продукты питания так, чтобы их концентрация была оптимальной и соответствовала нормам содержания витаминов в пище.
Обозначим оптимальную концентрацию (количество единиц) для продукта 1 как x1, для продукта 2 — как x2 и так далее. Так как мы будем смешивать продукты, то для каждого витамина (столбца таблицы) можно просто просуммировать значения, по всем продуктам. Учитывая, что сбалансированная диета должна включать 170 единиц витамина А, то, используя данные из столбца «Витамин А», составим уравнение:

Аналогичные уравнения можно составить и для витаминов B, C, D, E, объединив всё в систему:
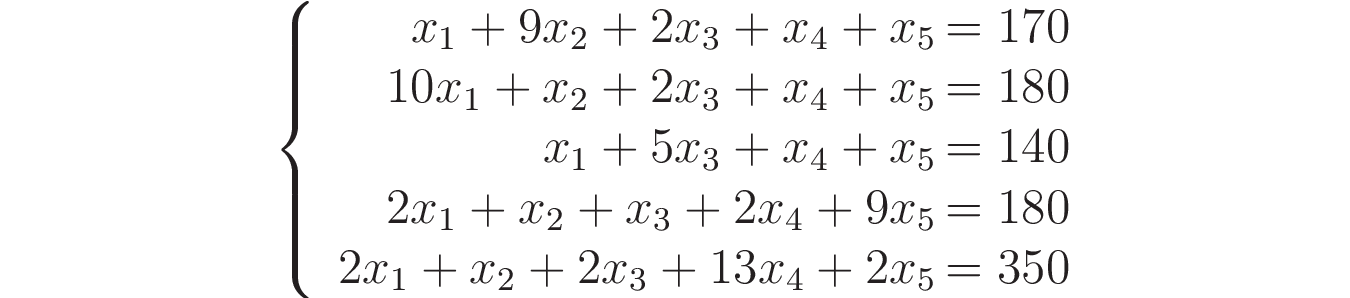
Запишем полученную СЛАУ в матричной форме:
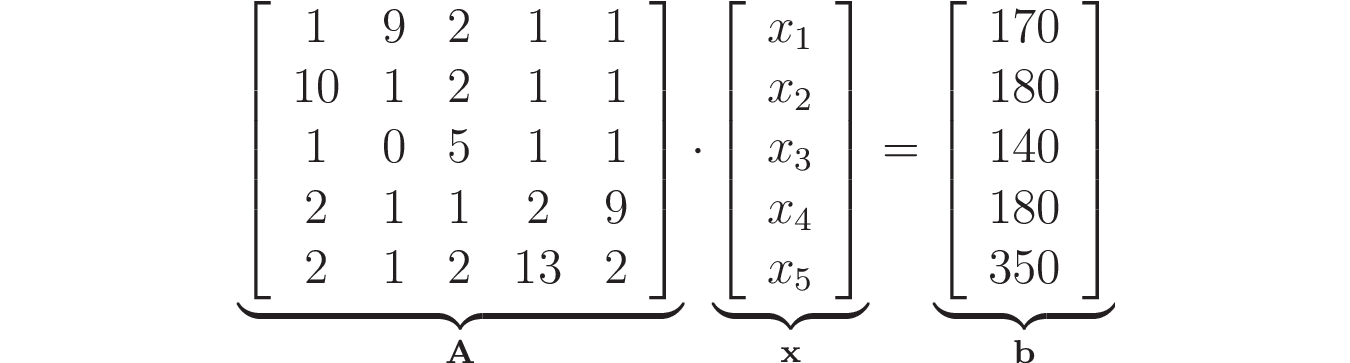
Теперь для решения системы можно использовать scipy.linalg.solve():
>>>
In [1]: import numpy as np
...: from scipy.linalg import solve
In [2]: A = np.array(
...: [
...: [1, 9, 2, 1, 1],
...: [10, 1, 2, 1, 1],
...: [1, 0, 5, 1, 1],
...: [2, 1, 1, 2, 9],
...: [2, 1, 2, 13, 2],
...: ]
...: )
In [3]: b = np.array([170, 180, 140, 180, 350]).reshape((5, 1))
In [4]: x = solve(A, b)
...: x
Out[4]:
array([[10.],
[10.],
[20.],
[20.],
[10.]])
Мы получили результат. Давайте его расшифруем. Сбалансированная диета должна включать:
Питайтесь правильно! Используйте scipy.linalg и будьте здоровы!
Источник статьи: https://habr.com/ru/company/macloud/blog/564154/
СЛАУ — мощный инструмент моделирования процессов. Если некая хорошо изученная модель на основе СЛАУ годится для формализации задачи, то с высокой вероятностью её можно будет решить. А вот насколько быстро — это зависит от вашего инструментария и вычислительных мощностей.
Я расскажу про один из таких инструментов — Python-пакет scipy.linalg из библиотеки SciPy, который позволяет быстро и эффективно решать многие задачи с использованием аппарата линейной алгебры.
В этом туториале вы узнаете:
- как установить scipy.linalg и подготовить среду выполнения кода;
- как работать с векторами и матрицами с помощью NumPy;
- почему scipy.linalg лучше, чем numpy.linalg;
- как формализовать задачи с использованием систем линейных алгебраических уравнений;
- как решать СЛАУ с помощью scipy.linalg (на реальном примере).
Если можно — сделай тут habraCUT! Важно, чтобы этот ^^ список люди прочитали и заинтересовались
Когда речь идёт о математике, изложение материала должно быть последовательным — таким, чтобы одно следовало из другого. Эта статья не исключение: сначала будет много подготовительной информации и только потом мы перейдём непосредственно к делу.
Если готовы к этому — приглашаю под кат. Хотя, честно говоря, некоторые разделы можно пропускать — например, основы работы с векторами и матрицами в NumPy (если вы хорошо знакомы с ним).
Установка scipy.linalg
SciPy — это библиотека Python с открытым исходным кодом для научных вычислений: решение СЛАУ, оптимизация, интеграция, интерполяция и обработка сигналов. Помимо linalg, она содержит несколько других пакетов — например, NumPy, Matplotlib, SymPy, IPython и pandas.
Среди прочего, scipy.linalg содержит функции для с работы с матрицами — вычисление определителя, инверсия, вычисление собственных значений и векторов, а также сингулярное разложение.
Чтобы использовать scipy.linalg, вам необходимо установить и настроить библиотеку SciPy. Это можно сделать с помощью дистрибутива Anaconda, а также системы управления пакетами и инсталлятора Conda.
Для начала подготовьте среду выполнения для библиотеки:
$ conda create --name linalg
$ conda activate linalg
Установите необходимые пакеты:
(linalg) $ conda install scipy jupyter
Эта команда может работать долго. Не пугайтесь!
Я предлагаю использовать Jupyter Notebook для запуска кода в интерактивной среде. Это не обязательно, но лично мне он облегчает работу.
Перед открытием Jupyter Notebook вам необходимо зарегистрировать экземпляр conda linalg, чтобы использовать его в качестве ядра при создании ноутбука. Для этого выполните следующую команду:
(linalg) $ python -m ipykernel install --user --name linalg
Теперь можно открыть Jupyter Notebook:
$ jupyter notebook
Когда он загрузится в вашем браузере, создайте новый notebook, нажав New → linalg:

Чтобы убедиться, что установка библиотеки SciPy прошла успешно, введите в ноутбуке:
>>>
In [1]: import scipy
NumPy для работы с векторами и матрицами (куда же без него)
Сложно переоценить роль векторов и матриц при решении технических задач и, в том числе, задач машинного обучения.
NumPy — это наиболее популярный пакет для работы с матрицами и векторами в Python. Часто его применяют в сочетании с scipy.linalg. Чтобы начать работу с матрицами и векторами, нужно импортировать пакет NumPy:
>>>
In [2]: import numpy as np
Для представления матриц и векторов NumPy использует специальный тип, называемый ndarray. Чтобы создать объект ndarray, вы можете использовать array ().
Например, вам нужно создать следующую матрицу:
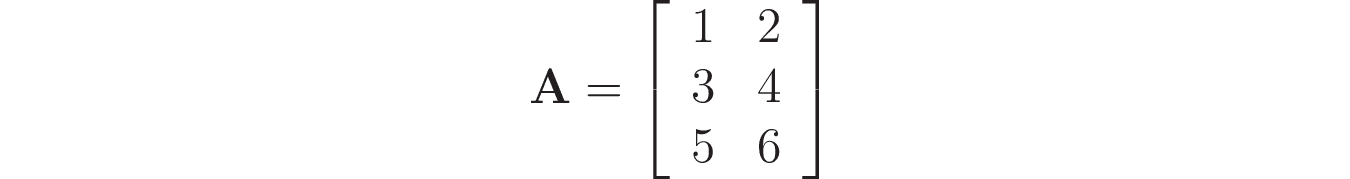
Создадим матрицу как набор вложенных списков (векторов-строк):
>>>
In [3]: A = np.array([[1, 2], [3, 4], [5, 6]])
...: A
Out[3]:
array([[1, 2],
[3, 4],
[5, 6]])
Заметьте, что приведённый выше вывод (Outp[3]) достаточно наглядно показывает получившуюся матрицу.
И ещё: все элементы матрицы должны и будут иметь один тип. Это можно проверить с помощью dtype.
>>>
In [4]: A.dtype
Out[4]:
dtype('int64')
Здесь элементы являются целыми числами, поэтому их общий тип по умолчанию — int64. Если бы среди них было хотя бы одно число с плавающей точкой, все элементы получили бы тип float64:
>>>
In [5]: A = np.array([[1.0, 2], [3, 4], [5, 6]])
...: A
Out[5]:
array([[1., 2.],
[3., 4.],
[5., 6.]])
In [6]: A.dtype
Out[6]:
dtype('float64')
Чтобы вывести на экран размерность матрицы, можно использовать метод shape:
>>>
In [7]: A.shape
Out[7]:
(3, 2)
Как и ожидалось, размерность матрицы A 3×2, то есть A имеет три строки и два столбца.
При работе с матрицами часто приходится использовать операцию транспонирования, которая столбцы превращает в строки и наоборот. Чтобы транспонировать вектор или матрицу (представленную объектом типа ndarray), вы можете использовать .transpose () или .T. Например:
>>>
In [8]: A.T
Out[8]:
array([[1., 3., 5.],
[2., 4., 6.]])
Чтобы создать вектор, также можно использовать.array(), передав туда список значений в качестве аргумента:
>>>
In [9]: v = np.array([1, 2, 3])
...: v
Out[9]:
array([1, 2, 3])
По аналогии с матрицами, используем .shape(), чтобы вывести на экран размерность вектора:
>>>
In [10]: v.shape
Out[10]:
(3,)
Заметьте, что она выглядит как (3,), а не как (3, 1) или (1, 3). Разработчики NumPy решили сделать отображение размерности векторов так же, как в MATLAB.
Чтобы получить на выходе размерность (1, 3), нужно было бы создать вот такой массив:
>>>
In [11]: v = np.array([[1, 2, 3]])
...: v.shape
Out[11]:
(1, 3)
Для (3, 1) — вот такой:
>>>
In [12]: v = np.array([[1], [2], [3]])
...: v.shape
Out[12]:
(3, 1)
Как видите, они не идентичны.
Часто возникает задача из вектора-строки сделать вектор-столбец. Как вариант, можно сначала создать вектор-строку, а потом использовать .reshape() для его преобразования в столбец:
>>>
In [13]: v = np.array([1, 2, 3]).reshape(3, 1)
...: v.shape
Out[13]:
(3, 1)
В приведённом выше примере мы использовали .reshape() для получения вектора-столбца с размерностью (3, 1) из вектора с размерностью(3,). Стоит отметить, что .reshape() делает преобразование с учётом того, что количество элементов (100% заполненных мест) в массиве с новой размерностью должно быть равно количеству элементов в исходном массиве.
В практических задачах часто требуется создавать матрицы, полностью состоящие из нулей, единиц или случайных чисел. Для этого NumPy предлагает несколько удобных функций, о которых я расскажу в следующем разделе.
Заполнение массивов данными
NumPy позволяет быстро создавать и заполнять массивы. Например, чтобы создать массив, заполненный нулями, можно использовать .zeros():
>>>
In [15]: A = np.zeros((3, 2))
...: A
Out[15]:
array([[0., 0.],
[0., 0.],
[0., 0.]])
В качестве аргумента .zeros() нужно указать размерность массива, упакованную в кортеж (перечислить значения через запятую и обернуть это в круглые скобки). Элементы созданного массива получат тип float64.
Точно так же, для создания массивов из единиц можно использовать .ones ():
>>>
In [16]: A = np.ones((2, 3))
...: A
Out[16]:
array([[1., 1., 1.],
[1., 1., 1.]])
Элементы созданного массива также получат тип float64.
Создать массив, заполненный случайными числами, поможет .random.rand():
>>>
In [17]: A = np.random.rand(3, 2)
...: A
Out[17]:
array([[0.8206045 , 0.54470809],
[0.9490381 , 0.05677859],
[0.71148476, 0.4709059 ]])
Говоря точнее, метод .random.rand() возвращает массив с псевдослучайными значениями (от 0 до 1) из множества, сгенерированного по закону равномерного распределения. Обратите внимание, что в отличие от .zeros() и .ones(), .random.rand () на вход принимает не кортеж, а просто два значения через запятую.
Чтобы получить массив с псевдослучайными значениями, взятыми из множества, сгенерированного по закону нормального распределения с нулевым средним и единичной дисперсией, вы можете использовать .random.randn():
>>>
In [18]: A = np.random.randn(3, 2)
...: A
Out[18]:
array([[-1.20019512, -1.78337814],
[-0.22135221, -0.38805899],
[ 0.17620202, -2.05176764]])
Почему scipy.linalg лучше, чем numpy.linalg
NumPy имеет встроенный модуль numpy.linalg для решения некоторых задач, связанных с аппаратом линейной алгебры. Обычно scipy.linalg рекомендуют использовать по следующим причинам:
- В официальной документации сказано, что scipy.linalg содержит все функции numpy.linalg, а также дополнительные функции, не входящие в numpy.linalg.
- В пакет scipy.linalg включена поддержка стандартов и библиотек BLAS (Basic Linear Algebra Subprograms) и LAPACK (Linear Algebra PACKage). Они позволяют выполнять алгебраические операции с оптимизацией вычислений. В numpy.linalg BLAS и LAPACK по умолчанию не включены. Поэтому, чаще всего, из коробки scipy.linalg работает быстрее, чем numpy.linalg.
Несмотря на то, что SciPy добавит зависимости в ваш проект, по возможности, используйте scipy.linalg вместо numpy.linalg.
В следующем разделе мы применим scipy.linalg для работы с системами линейных алгебраических уравнений. Наконец-то практика!
Формализация и решение задач с scipy.linalg
Пакет scipy.linalg может стать полезным инструментом для решения транспортной задачи, балансировки химических уравнений и электрических нагрузок, полиномиальной интерполяции и так далее.
В этом разделе вы узнаете, как использовать scipy.linalg.solve() для решения СЛАУ. Но прежде чем приступить к работе с кодом, займёмся формализацией задачи и далее рассмотрим простой пример.
Система линейных алгебраических уравнений — это набор из m уравнений, n переменных и вектора свободных членов. Прилагательное «линейных» означает, что все переменные имеют первую степень. Для простоты рассмотрим СЛАУ, где m и n равны 3:
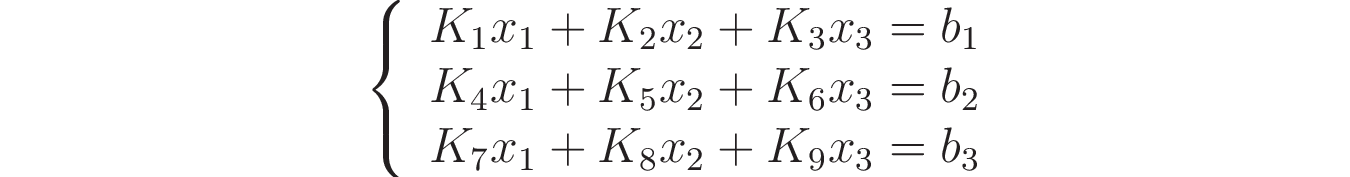
Есть ещё одно требование к «линейности»: коэффициенты K₁ … K₉ и вектор b₁ … b₃ должны быть константами (в математическом смысле этого слова).
В реальных задачах СЛАУ обычно содержат большое количество переменных, что делает невозможным решение систем вручную. К счастью, такие инструменты, как scipy.linalg, могут выполнить эту тяжелую работу.
Задача 1
Мы сначала разберёмся с основами scipy.linalg.solve() на простом примере, а в следующем разделе возьмём задачу посложнее.
Итак:
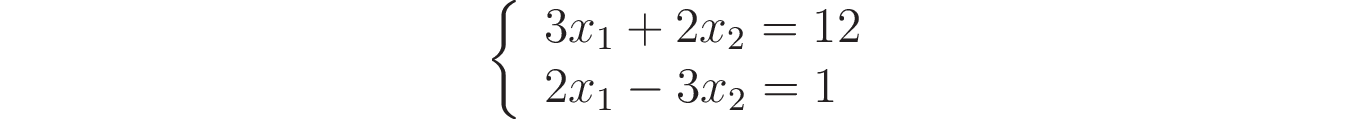
Перейдём к матричной записи нашей системы и введём соответствующие обозначения — A, x и b:

Заметьте: левая часть в исходной записи системы — это обычное произведение матрицы A на вектор x.
Всё, теперь можно переходить к программированию.
Пишем код, используя scipy.linalg.solve()
Входными данными для scipy.linalg.solve() будут матрица A и вектор b. Их нужно представить в виде двух массивов: A — массив 2х2 и b — массив 2х1. В этом нам как раз поможет NumPy. Таким образом, мы можем решить систему так:
>>>
1In [1]: import numpy as np
2 ...: from scipy.linalg import solve
3
4In [2]: A = np.array(
5 ...: [
6 ...: [3, 2],
7 ...: [2, -1],
8 ...: ]
9 ...: )
10
11In [3]: b = np.array([12, 1]).reshape((2, 1))
12
13In [4]: x = solve(A, b)
14 ...: x
15 Out[4]:
16 array([[2.],
17 [3.]])
Разберём приведённый выше код:
- Строки 1 и 2: импортируем NumPy и функцию solve() из scipy.linalg.
- Строки с 4 по 9: создаём матрицу коэффициентов как двумерный массив с именем A.
- Строка 11: создаём вектор-строку b как массив с именем b. Чтобы сделать его вектор-столбцом, вызываем .reshape ((2, 1)).
- Строки 13 и 14: вызываем .solve() для нашей системы, результат сохраняем в х и выводим его. Обратите внимание, что .solve() возвращает вектор из чисел с плавающей запятой, даже если все элементы исходных массивов являются целыми числами.
Если вы подставите x1 = 2 и x2 = 3 в исходные уравнения, будет ясно, что это действительно решение нашей системы.
Далее возьмём более сложный пример из реальной практики.
Задача 2: составление плана питания
Это одна из типовых задач, встречающихся на практике: найти пропорции компонентов для получения определенной смеси.
Ниже мы сформируем план питания, смешивая разные продукты, чтобы получить сбалансированную диету.
Нам даны нормы содержания витаминов в пище:
- 170 единиц витамина А;
- 180 единиц витамина B;
- 140 единиц витамина С;
- 180 единиц витамина D;
- 350 единиц витамина Е.
В следующей таблице представлены результаты анализа продуктов. В одном грамме каждого продукта содержится некоторое количество витаминов:
| Продукт | Витамин A | Витамин B | Витамин C | Витамин D | Витамин E |
| 1 | 1 | 10 | 1 | 2 | 2 |
| 2 | 9 | 1 | 0 | 1 | 1 |
| 3 | 2 | 2 | 5 | 1 | 2 |
| 4 | 1 | 1 | 1 | 2 | 13 |
| 5 | 1 | 1 | 1 | 9 | 2 |
Необходимо скомбинировать продукты питания так, чтобы их концентрация была оптимальной и соответствовала нормам содержания витаминов в пище.
Обозначим оптимальную концентрацию (количество единиц) для продукта 1 как x1, для продукта 2 — как x2 и так далее. Так как мы будем смешивать продукты, то для каждого витамина (столбца таблицы) можно просто просуммировать значения, по всем продуктам. Учитывая, что сбалансированная диета должна включать 170 единиц витамина А, то, используя данные из столбца «Витамин А», составим уравнение:

Аналогичные уравнения можно составить и для витаминов B, C, D, E, объединив всё в систему:
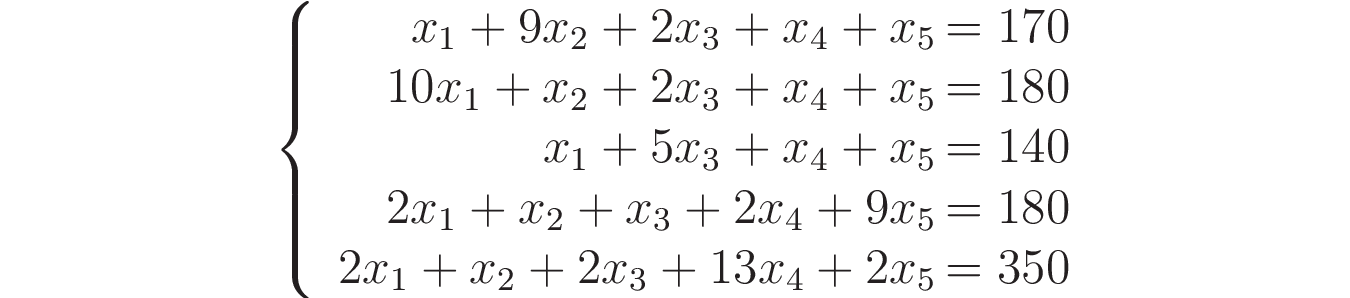
Запишем полученную СЛАУ в матричной форме:
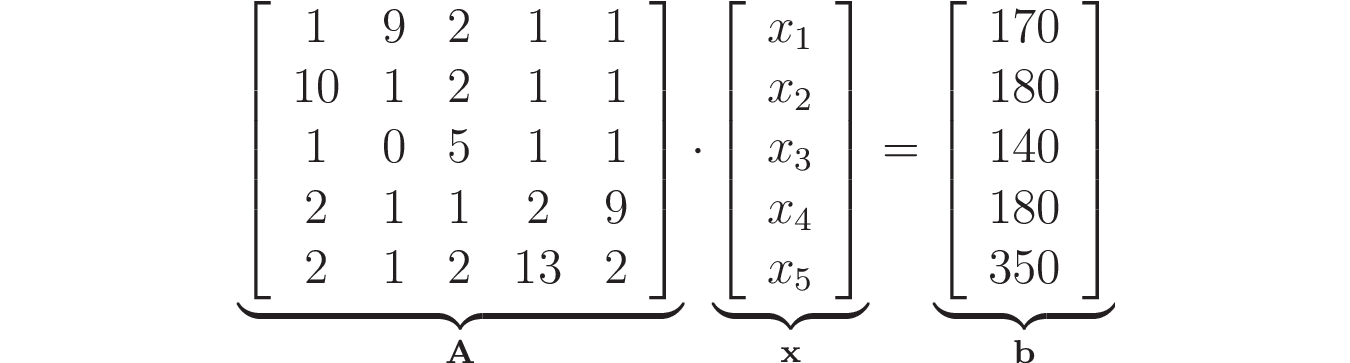
Теперь для решения системы можно использовать scipy.linalg.solve():
>>>
In [1]: import numpy as np
...: from scipy.linalg import solve
In [2]: A = np.array(
...: [
...: [1, 9, 2, 1, 1],
...: [10, 1, 2, 1, 1],
...: [1, 0, 5, 1, 1],
...: [2, 1, 1, 2, 9],
...: [2, 1, 2, 13, 2],
...: ]
...: )
In [3]: b = np.array([170, 180, 140, 180, 350]).reshape((5, 1))
In [4]: x = solve(A, b)
...: x
Out[4]:
array([[10.],
[10.],
[20.],
[20.],
[10.]])
Мы получили результат. Давайте его расшифруем. Сбалансированная диета должна включать:
- 10 единиц продукта 1;
- 10 единиц продукта 2;
- 20 единиц продукта 3;
- 20 единиц продукта 4;
- 10 единиц продукта 5.
Питайтесь правильно! Используйте scipy.linalg и будьте здоровы!
Источник статьи: https://habr.com/ru/company/macloud/blog/564154/
