Выборки и популяции
В статистической науке термины «выборка» и «популяция» имеют особое значение. Популяция, или генеральная совокупность, — это все множество объектов, которые исследователь хочет понять или в отношении которых сделать выводы. Например, во второй половине 19-го века основоположник генетики Грегор Йохан Мендель) записывал наблюдения о растениях гороха. Несмотря на то, что он изучал в лабораторных условиях вполне конкретные сорта растения, его задача состояла в том, чтобы понять базовые механизмы, лежащие в основе наследственности абсолютно всех возможных сортов гороха.В статистической науке о группе объектов, из которых извлекается выборка, говорят, как о популяции, независимо от того, являются изучаемые объекты живыми существами или нет.
Поскольку популяция может быть крупной — или бесконечной, как в случае растений гороха Менделя — мы должны изучать репрезентативные выборки, и на их основе делать выводы о всей популяции в целом. В целях проведения четкого различия между поддающимися измерению атрибутами выборок и недоступными атрибутами популяции, мы используем термин статистики, имея при этом в виду атрибуты выборки, и говорим о параметрах, имея в виду атрибуты популяции.
Статистики — это атрибуты, которые мы можем измерить на основе выборок. Параметры — это атрибуты популяции, которые мы пытаемся вывести статистически.
В действительности, статистики и параметры различаются в силу применения разных символов в математических формулах:
| Мера | Выборочная статистика | Популяционный параметр |
| Объем | n | N |
| Среднее значение | x̅ | μx |
| Стандартное отклонение | Sx | σx |
| Стандартная ошибка | Sx̅ |
Теперь вычислим стандартную ошибку средних значений за определенный день. Например, возьмем конкретный день, скажем, 1 мая:
def ex_2_8():
'''Вычислить стандартную ошибку
средних значений за определенный день'''
may_1 = '2015-05-01'
df = with_parsed_date( load_data('dwell-times.tsv') )
filtered = df.set_index( ['date'] )[may_1]
se = standard_error( filtered['dwell-time'] )
print('Стандартная ошибка:', se)
Стандартная ошибка: 3.627340273094217
Хотя мы взяли выборку всего из одного дня, вычисляемая нами стандартная ошибка очень близка к стандартному отклонению всех выборочных средних — 3.6 сек. против 3.7 сек. Это, как если бы, подобно клетке, содержащей ДНК, в каждой выборке была закодирована информация обо всей находящейся внутри нее популяции.
Интервалы уверенности
Поскольку стандартная ошибка выборки измеряет степень близости, с которой, по нашим ожиданиям, выборочное среднее соответствует среднему популяционному, то мы можем также рассмотреть обратное — стандартная ошибка измеряет степень близосто, с которой, по нашим ожиданиям, популяционное среднее соответствует измеренному среднему выборочному. Другими словами, на основе стандартной ошибки мы можем вывести, что популяционное среднее находится в пределах некого ожидаемого диапазона выборочного среднего с некоторой степенью уверенности.Понятия «степень уверенности» и «ожидаемый диапазон», взятые вместе, дают определение термину интервал уверенности.
При установлении интервалов уверенности обычной практикой является задание интервала размером 95% — мы на 95% уверены, что популяционный параметр находится внутри интервала. Разумеется, еще остается 5%-я возможность, что он там не находится.
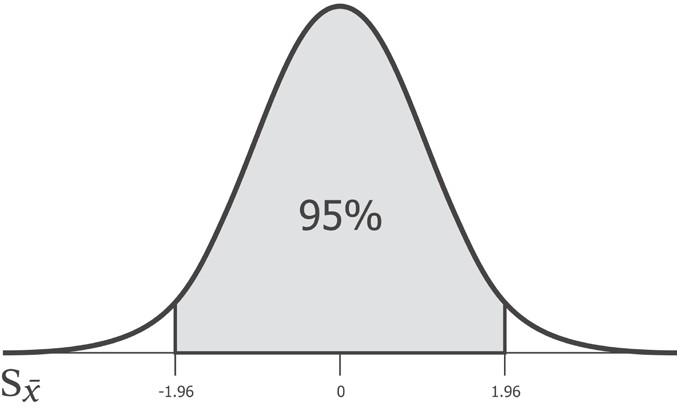
Какой бы ни была стандартная ошибка, 95% популяционного среднего значения будет находиться между -1.96 и 1.96 стандартных отклонений от выборочного среднего. И, следовательно, число 1.96 является критическим значением для 95%-ого интервала уверенности. Это критическое значение носит название z-значения.
Название z-значение вызвано тем, что нормальное распределение называется z-распределением. Впрочем, иногда z-значение так и называют — гауссовым значением.
Число 1.96 используется так широко, что его стоит запомнить. Впрочем, критическое значение мы можем вычислить сами, воспользовавшись функцией scipy stats.norm.ppf. Приведенная ниже функция confidence_interval ожидает значение для p между 0 и 1. Для нашего 95%-ого интервала уверенности оно будет равно 0.95. В целях вычисления положения каждого из двух хвостов нам нужно вычесть это число из единицы и разделить на 2 (2.5% для интервала уверенности шириной 95%):
def confidence_interval(p, xs):
'''Интервал уверенности'''
mu = xs.mean()
se = standard_error(xs)
z_crit = stats.norm.ppf(1 - (1-p) / 2)
return [mu - z_crit * se, mu + z_crit * se]
def ex_2_9():
'''Вычислить интервал уверенности
для данных за определенный день'''
may_1 = '2015-05-01'
df = with_parsed_date( load_data('dwell-times.tsv') )
filtered = df.set_index( ['date'] )[may_1]
ci = confidence_interval(0.95, filtered['dwell-time'])
print('Интервал уверенности: ', ci)
Интервал уверенности: [83.53415272762004, 97.753065317492741]
Полученный результат говорит о том, что можно на 95% быть уверенным в том, что популяционное среднее находится между 83.53 и 97.75 сек. И действительно, популяционное среднее, которое мы вычислили ранее, вполне укладывается в этот диапазон.
Сравнение выборок
После вирусной маркетинговой кампании веб-команда в AcmeContent извлекает для нас однодневную выборку времени пребывания посетителей на веб-сайте для проведения анализа. Они хотели бы узнать, не привлекла ли их недавняя кампания более активных посетителей веб-сайта. Интервалы уверенности предоставляют нам интуитивно понятный подход к сравнению двух выборок.Точно так же, как мы делали ранее, мы загружаем значения времени пребывания, полученные в результате маркетинговой кампании, и их резюмируем:
def ex_2_10():
'''Сводные статистики данных, полученных
в результате вирусной кампании'''
ts = load_data('campaign-sample.tsv')['dwell-time']
print('n: ', ts.count())
print('Среднее: ', ts.mean())
print('Медиана: ', ts.median())
print('Стандартное отклонение: ', ts.std())
print('Стандартная ошибка: ', standard_error(ts))
ex_2_10()
n: 300
Среднее: 130.22
Медиана: 84.0
Стандартное отклонение: 136.13370714388034
Стандартная ошибка: 7.846572839994115
Среднее значение выглядит намного больше, чем то, которое мы видели ранее — 130 сек. по сравнению с 90 сек. Вполне возможно, здесь имеется некое значимое расхождение, хотя стандартная ошибка более чем в 2 раза больше той, которая была в предыдущей однодневной выборке, в силу меньшего размера выборки и большего стандартного отклонения. Основываясь на этих данных, можно вычислить 95%-й интервал уверенности для популяционного среднего, воспользовавшись для этого той же самой функцией confidence_interval, что и прежде:
def ex_2_11():
'''Интервал уверенности для данных,
полученных в результате вирусной кампании'''
ts = load_data('campaign-sample.tsv')['dwell-time']
print('Интервал уверенности:', confidence_interval(0.95, ts))
Интервал уверенности: [114.84099983154137, 145.59900016845864]
95%-ый интервал уверенности для популяционного среднего лежит между 114.8 и 145.6 сек. Он вообще не пересекается с вычисленным нами ранее популяционным средним в размере 90 сек. Похоже, имеется какое-то крупное расхождение с опорной популяцией, которое едва бы произошло по причине одной лишь ошибки выборочного обследования. Наша задача теперь состоит в том, чтобы выяснить почему это происходит.
Ошибка выборочного обследования, также систематическая ошибка при взятии выборки, возникает, когда статистические характеристики популяции оцениваются исходя из подмножества этой популяции.
Искаженность
Выборка должна быть репрезентативной, то есть представлять популяцию, из которой она взята. Другими словами, при взятии выборки необходимо избегать искажения, которое происходит в результате того, что отдельно взятые члены популяции систематически из нее исключаются (либо в нее включаются) по сравнению с другими.Широко известным примером искажения при взятии выборки является опрос населения, проведенный в США еженедельным журналом «Литературный Дайджест» (Literary Digest) по поводу президентских выборов 1936 г. Это был один из самых больших и самых дорогостоящих когда-либо проводившихся опросов: тогда по почте было опрошено 2.4 млн. человек. Результаты были однозначными — губернатор-республиканец от шт. Канзас Альфред Лэндон должен был победить Франклина Д. Рузвельта с 57% голосов. Как известно, в конечном счете на выборах победил Рузвельт с 62% голосов.
Первопричина допущенной журналом огромной ошибки выборочного обследования состояла в искажении при отборе. В своем стремлении собрать как можно больше адресов избирателей журнал «Литературный Дайджест» буквально выскреб все телефонные справочники, подписные перечни журнала и списки членов клубов. В эру, когда телефоны все еще во многом оставались предметом роскоши, такая процедура гарантировано имела избыточный вес в пользу избирателей, принадлежавших к верхнему и среднему классам, и не был представительным для электората в целом. Вторичной причиной искажения стала искаженность в результате неответов — в опросе фактически согласились участвовать всего менее четверти тех, к кому обратились. В этом виде искаженности при отборе предпочтение отдается только тем респондентам, которые действительно желают принять участие в голосовании.
Распространенный способ избежать искаженности при отборе состоит в том, чтобы каким-либо образом рандомизировать выборку. Введение в процедуру случайности делает вряд ли возможным, что экспериментальные факторы окажут неправомерное влияние на качество выборки. Опрос населения еженедельником «Литературный Дайджест» был сосредоточен на получении максимально возможной выборки, однако неискаженная малая выборка была бы намного полезнее, чем плохо отобранная большая выборка.
Если мы откроем файл campaign_sample.tsv, то обнаружим, что наша выборка приходится исключительно на 6 июня 2015 года. Это был выходной день, и этот факт мы можем легко подтвердить при помощи функции pandas:
'''Проверка даты'''
d = pd.to_datetime('2015 6 6')
d.weekday() in [5,6]
True
Все наши сводные статистики до сих пор основывались на данных, которые мы отфильтровывали для получения только рабочих дней. Искаженность в нашей выборке вызвана именно этим фактом, и, если окажется, что поведение посетителей в выходные отличается от поведения в будние дни — вполне возможный сценарий — тогда мы скажем, что выборки представляют две разные популяции.
Визуализация разных популяций
Теперь снимем фильтр для рабочих дней и построим график среднесуточного времени пребывания для всех дней недели — рабочих и выходных:def ex_2_12():
'''Построить график времени ожидания
по всем дням, без фильтра'''
df = load_data('dwell-times.tsv')
means = mean_dwell_times_by_date(df)['dwell-time']
means.hist(bins=20)
plt.xlabel('Ежедневное время ожидания неотфильтрованное, сек.')
plt.ylabel('Частота')
plt.show()
Этот пример сгенерирует следующую ниже гистограмму:
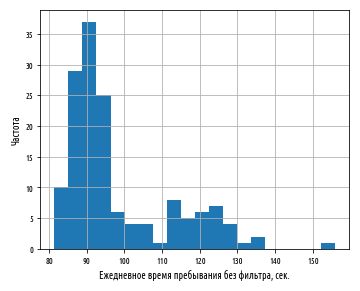
Распределение уже не является нормальным. Оно фактически является бимодальным, поскольку у него два пика. Второй меньший пик соответствует вновь добавленным выходным дням, и он ниже потому что количество выходных дней гораздо меньше количества рабочих дней, а также потому что стандартная ошибка распределения больше.
Распределения более чем с одним пиком обычно называются мультимодальными. Они могут указывать на совмещение двух или более нормальных распределений, и, следовательно, возможно, на совмещение двух или более популяций. Классическим примером бимодальности является распределение показателей роста людей, поскольку модальный рост мужчин выше, чем у женщин.
Данные выходных дней имеют другие характеристики в отличие от данных будних дней. Мы должны удостовериться, что мы сравниваем подобное с подобным. Отфильтруем наш первоначальный набор данных только по выходным дням:
def ex_2_13():
'''Сводные статистики данных,
отфильтрованных только по выходным дням'''
df = with_parsed_date( load_data('dwell-times.tsv') )
df.index = df['date']
df = df[df['date'].index.dayofweek > 4] # суббота-воскресенье
weekend_times = df['dwell-time']
print('n: ', weekend_times.count())
print('Среднее: ', weekend_times.mean())
print('Медиана: ', weekend_times.median())
print('Стандартное отклонение: ', weekend_times.std())
print('Стандартная ошибка: ', standard_error(weekend_times))
n: 5860
Среднее: 117.78686006825939
Медиана: 81.0
Стандартное отклонение: 120.65234077179436
Стандартная ошибка: 1.5759770362547678
Итоговое среднее значение в выходные дни (на основе 6-ти месячных данных) составляет 117.8 сек. и попадает в пределы 95%-ого интервала уверенности для маркетинговой выборки. Другими словами, хотя среднее значение времени пребывания в размере 130 сек. является высоким даже для выходных, расхождение не настолько большое, что его нельзя было бы приписать простой случайной изменчивости в выборке.
Мы только что применили подход к установлению подлинного расхождения в популяциях (между посетителями веб-сайта в выходные по сравнению с посетителями в будние дни), который при проведении проверки обычно не используется. Более традиционный подход начинается с выдвижения гипотетического предположения, после чего это предположение сверяется с данными. Для этих целей статистический метод анализа определяет строгий подход, который называется проверкой статистических гипотез.
Это и будет темой следующего поста, поста №3.
Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.
Источник статьи: https://habr.com/ru/post/556806/