Регрессия
Хотя, возможно, и полезно знать, что две переменные коррелируют, мы не можем использовать лишь одну эту информацию для предсказания веса олимпийских пловцов при наличии данных об их росте или наоборот. При установлении корреляции мы измерили силу и знак связи, но не наклон, т.е. угловой коэффициент. Для генерирования предсказания необходимо знать ожидаемый темп изменения одной переменной при заданном единичном изменении в другой.Мы хотели бы вывести уравнение, связывающее конкретную величину одной переменной, так называемой независимой переменной, с ожидаемым значением другой, зависимой переменной. Например, если наше линейное уравнение предсказывает вес при заданном росте, то рост является нашей независимой переменной, а вес — зависимой.
Описываемые этими уравнениями линии называются линиями регрессии. Этот Термин был введен британским эрудитом 19-ого века сэром Фрэнсисом Гэлтоном. Он и его студент Карл Пирсон, который вывел коэффициент корреляции, в 19-ом веке разработали большое количество методов, применяемых для изучения линейных связей, которые коллективно стали известны как методы регрессионного анализа.
Вспомним, что из корреляции не следует причинная обусловленность, причем термины «зависимый» и «независимый» не означают никакой неявной причинной обусловленности. Они представляют собой всего лишь имена для входных и выходных математических значений. Классическим примером является крайне положительная корреляция между числом отправленных на тушение пожара пожарных машин и нанесенным пожаром ущербом. Безусловно, отправка пожарных машин на тушение пожара сама по себе не наносит ущерб. Никто не будет советовать сократить число машин, отправляемых на тушение пожара, как способ уменьшения ущерба. В подобных ситуациях мы должны искать дополнительную переменную, которая была бы связана с другими переменными причинной связью и объясняла корреляцию между ними. В данном примере это может быть размер пожара. Такие скрытые причины называются спутывающими переменными, потому что они искажают нашу возможность определять связь между зависимыми переменными.
Линейные уравнения
Две переменные, которые мы можем обозначить как x и y, могут быть связаны друг с другом строго или нестрого. Самая простая связь между независимой переменной x и зависимой переменной y является прямолинейной, которая выражается следующей формулой:Здесь значения параметров a и b определяют соответственно точную высоту и крутизну прямой. Параметр a называется пересечением с вертикальной осью или константой, а b — градиентом, наклоном линии или угловым коэффициентом. Например, в соотнесенности между температурными шкалами по Цельсию и по Фаренгейту a = 32 и b = 1.8. Подставив в наше уравнение значения a и b, получим:
Для вычисления 10°С по Фаренгейту мы вместо x подставляем 10:
Таким образом, наше уравнение сообщает, что 10°С равно 50°F, и это действительно так. Используя Python и возможности визуализации pandas, мы можем легко написать функцию, которая переводит градусы из Цельсия в градусы Фаренгейта и выводит результат на график:
'''Функция перевода из градусов Цельсия в градусы Фаренгейта'''
celsius_to_fahrenheit = lambda x: 32 + (x * 1.8)
def ex_3_11():
'''График линейной зависимости температурных шкал'''
df = pd.DataFrame({'C':s, 'F':s.map(celsius_to_fahrenheit)})
df.plot('C', 'F', legend=False, grid=True)
plt.xlabel('Градусы Цельсия')
plt.ylabel('Градусы Фаренгейта')
plt.show()
Этот пример сгенерирует следующий ниже линейный график:
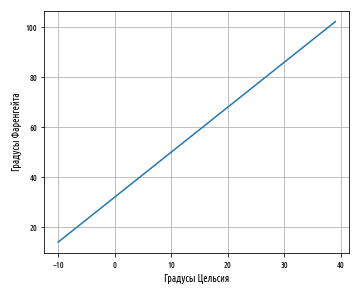
Обратите внимание, как синяя линия пересекает 0 на шкале Цельсия при величине 32 на шкале Фаренгейта. Пересечение a — это значение y, при котором значение x равно 0.
Наклон линии с неким угловым коэффициентом определяется параметром b; в этом уравнении его значение близко к 2. Как видно, диапазон шкалы Фаренгейта почти вдвое шире диапазона шкалы Цельсия. Другими словами, прямая устремляется вверх по вертикали почти вдвое быстрее, чем по горизонтали.
Остатки
К сожалению, немногие связи столь же чистые, как перевод между градусами Цельсия и Фаренгейта. Прямолинейное уравнение редко позволяет нам определять y строго в терминах x. Как правило, будет иметься ошибка, и, таким образом, уравнение примет следующий вид:Здесь, ε — это ошибка или остаточный член, обозначающий расхождение между значением, вычисленным параметрами a и b для данного значения x и фактическим значением y. Если предсказанное значение y — это ŷ, то ошибка — это разность между обоими:
Такая ошибка называется остатком. Остаток может возникать из-за случайных факторов, таких как погрешность измерения, либо неслучайных факторов, которые неизвестны. Например, если мы пытаемся предсказать вес как функцию роста, то неизвестные факторы могут состоять из диеты, уровня физической подготовки и типа телосложения (либо просто эффекта округления до самого близкого килограмма).
Если для a и b мы выберем неидеальные параметры, то остаток для каждого x будет больше, чем нужно. Из этого следует, что параметры, которые мы бы хотели найти, должны минимизировать остатки во всех значениях x и y.
Обычные наименьшие квадраты
Для того, чтобы оптимизировать параметры линейной модели, мы бы хотели создать функцию стоимости, так называемую функцией потери, которая количественно выражает то, насколько близко наши предсказания укладывается в данные. Мы не можем просто взять и просуммировать положительные и отрицательные остатки, потому что даже самые большие остатки обнулят друг друга, если их знаки противоположны.Прежде, чем вычислить сумму, мы можем возвести значения в квадрат, чтобы положительные и отрицательные остатки учитывались в стоимости. Возведение в квадрат также создает эффект наложения большего штрафа на большие ошибки, чем на меньшие ошибки, но не настолько много, чтобы самый большой остаток всегда доминировал.
Выражаясь в терминах задачи оптимизации, мы стремимся выявить коэффициенты, которые минимизируют сумму квадратов остатков. Этот метод называется обычными наименьшими квадратами, от англ. Ordinary Least Squares (OLS), и формула для вычисления наклона линии регрессии по указанному методу выглядит так:

Хотя она выглядит сложнее предыдущих уравнений, на самом деле, эта формула представляет собой всего лишь сумму квадратов остатков, деленную на сумму квадратов отклонений от среднего значения. В данном уравнении используется несколько членов из других уравнений, которые уже рассматривались, и мы можем его упростить, приведя к следующему виду:
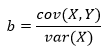
Пересечение (a) — это член, позволяющий прямой с заданным наклоном проходить через среднее значение X и Y:
Значения a и b — это коэффициенты, получаемые в результате оценки методом обычных наименьших квадратов.
Наклон и пересечение
Мы уже рассматривали функции covariance, varianceи mean, которые нужны для вычисления наклона прямой и точки пересечения для данных роста и веса пловцов. Поэтому вычисление наклона и пересечения имеют тривиальный вид:def slope(xs, ys):
'''Вычисление наклона линии (углового коэффициента)'''
return xs.cov(ys) / xs.var()
def intercept(xs, ys):
'''Вычисление точки пересечения (с осью Y)'''
return ys.mean() - (xs.mean() * slope(xs, ys))
def ex_3_12():
'''Вычисление пересечения и наклона (углового коэффициента)
на примере данных роста и веса'''
df = swimmer_data()
X = df['Рост, см']
y = df['Вес'].apply(np.log)
a = intercept(X, y)
b = slope(X, y)
print('Пересечение: %f, наклон: %f' % (a,b))
Пересечение: 1.691033, наклон: 0.014296
В результате будет получен наклон приблизительно 0.0143 и пересечение приблизительно 1.6910.
Интерпретация
Величина пересечения — это значение зависимой переменной (логарифмический вес), когда независимая переменная (рост) равна нулю. Для получения этого значения в килограммах мы можем воспользоваться функцией np.exp, обратной для функции np.log. Наша модель дает основания предполагать, что вероятнее всего вес олимпийского пловца с нулевым ростом будет 5.42 кг. Разумеется, такое предположение лишено всякого смысла, к тому же экстраполяция за пределы границ тренировочных данных является не самым разумным решением.Величина наклона показывает, насколько y изменяется для каждой единицы изменения в x. Модель исходит из того, что каждый дополнительный сантиметр роста прибавляет в среднем 1.014 кг. веса олимпийских пловцов. Поскольку наша модель основывается на данных о всех олимпийских пловцах, она представляет собой усредненный эффект от увеличения в росте на единицу без учета любого другого фактора, такого как возраст, пол или тип телосложения.
Визуализация
Результат линейного уравнения можно визуализировать при помощи имплементированной ранее функции regression_line и простой функции от x, которая вычисляет ŷ на основе коэффициентов a и b.'''Функция линии регрессии'''
regression_line = lambda a, b: lambda x: a + (b * x) # вызовы fn(a,b)(x)
def ex_3_13():
'''Визуализация линейного уравнения
на примере данных роста и веса'''
df = swimmer_data()
X = df['Рост, см'].apply( jitter(0.5) )
y = df['Вес'].apply(np.log)
a, b = intercept(X, y), slope(X, y)
ax = pd.DataFrame(np.array([X, y]).T).plot.scatter(0, 1, s=7)
s = pd.Series(range(150,210))
df = pd.DataFrame( {0:s, 1:s.map(regression_line(a, b))} )
df.plot(0, 1, legend=False, grid=True, ax=ax)
plt.xlabel('Рост, см.')
plt.ylabel('Логарифмический вес')
plt.show()
Функция regression_line возвращает функцию от x, которая вычисляет a + bx.
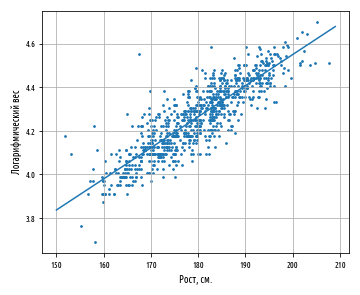
Указанная функция может также использоваться для вычисления каждого остатка, показывая степень, с которой наша оценка ŷ отклоняется от каждого измеренного значения y.
def residuals(a, b, xs, ys):
'''Вычисление остатков'''
estimate = regression_line(a, b) # частичное применение
return pd.Series( map(lambda x, y: y - estimate(x), xs, ys) )
constantly = lambda x: 0
def ex_3_14():
'''Построение графика остатков на примере данных роста и веса'''
df = swimmer_data()
X = df['Рост, см'].apply( jitter(0.5) )
y = df['Вес'].apply(np.log)
a, b = intercept(X, y), slope(X, y)
y = residuals(a, b, X, y)
ax = pd.DataFrame(np.array([X, y]).T).plot.scatter(0, 1, s=12)
s = pd.Series(range(150,210))
df = pd.DataFrame( {0:s, 1:s.map(constantly)} )
df.plot(0, 1, legend=False, grid=True, ax=ax)
plt.xlabel('Рост, см.')
plt.ylabel('Остатки')
plt.show()
График остатков — это график, который показывает остатки на оси Y и независимую переменную на оси X. Если точки на графике остатков разбросаны произвольно по обе стороны от горизонтальной оси, то линейная модель хорошо подогнана к нашим данным:
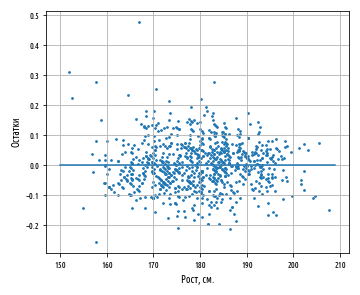
За исключением нескольких выбросов на левой стороне графика, график остатков, по-видимому, показывает, что линейная модель хорошо подогнана к данным. Построение графика остатков имеет важное значение для получения подтверждения, что линейная модель применима. В линейной модели используются некоторые допущения относительно данных, которые при их нарушении делают не валидными модели, которые вы строите.
Допущения
Первостепенное допущение линейной регрессии состоит в том, что, безусловно, существует линейная зависимость между зависимой и независимой переменной. Кроме того, остатки не должны коррелировать друг с другом либо с независимой переменной. Другими словами, мы ожидаем, что ошибки будут иметь нулевое среднее и постоянную дисперсию по отношению к зависимой и независимой переменной. График остатков позволяет быстро устанавливать, является ли это действительно так.Левая сторона нашего графика имеет более крупные значения остатков, чем правая сторона. Это соответствует большей дисперсии веса среди более низкорослых спортсменов. Когда дисперсия одной переменной изменяется относительно другой, говорят, что переменные гетероскедастичны, т.е. их дисперсия неоднородна. Этот факт представляет в регрессионном анализе проблему, потому что делает не валидным допущение в том, что модельные ошибки не коррелируют и нормально распределены, и что их дисперсии не варьируются вместе с моделируемыми эффектами.
Гетероскедастичность остатков здесь довольно мала и особо не должна повлиять на качество нашей модели. Если дисперсия на левой стороне графика была бы более выраженной, то она привела бы к неправильной оценке дисперсии методом наименьших квадратов, что в свою очередь повлияло бы на выводы, которые мы делаем, основываясь на стандартной ошибке.
Качество подгонки и R-квадрат
Хотя из графика остатков видно, что линейная модель хорошо вписывается в данные, т.е. хорошо к ним подогнана, было бы желательно количественно измерить качество этой подгонки. R2, или R-квадрат, варьируется в интервале между 0 и 1 и обозначает объяснительную мощность линейной регрессионной модели. Он вычисляет объясненную долю изменчивости в зависимой переменной.Обычно, чем ближе R2 к 1, тем лучше линия регрессии подогнана к точкам данных и больше изменчивости в Y объясняется независимой переменной X. R2 можно вычислить с помощью следующей ниже формулы:
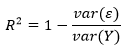
Здесь var(ε) — это дисперсия остатков и var(Y) — дисперсия в Y. В целях понимания смысла этой формулы допустим, что вы пытаетесь угадать чей-то вес. Если вам больше ничего неизвестно об испытуемых, то наилучшей стратегией будет угадывать среднее значение весовых данных внутри популяции в целом. Таким путем средневзвешенная квадратичная ошибка вашей догадки в сравнении с истинным весом будет var(Y), т.е. дисперсией данных веса в популяции.
Но если бы я сообщил вам их рост, то в соответствии с регрессионной моделью вы бы предположили, что a + bx. В этом случае вашей средневзвешенной квадратичной ошибкой было бы или дисперсия остатков модели.
Компонент формулы var(ε)/var(Y) — это соотношение средневзвешенной квадратичной ошибки с объяснительной переменной и без нее, т. е. доля изменчивости, оставленная моделью без объяснения. Дополнение R2 до единицы — это доля изменчивости, объясненная моделью.
Как и в случае с r, низкий R2 не означает, что две переменные не коррелированы. Просто может оказаться, что их связь не является линейной.
Значение R2 описывает качество подгонки линии регрессии к данным. Оптимально подогнанная линия — это линия, которая минимизирует значение R2. По мере удаления либо приближения от своих оптимальных значений R2 всегда будет расти.
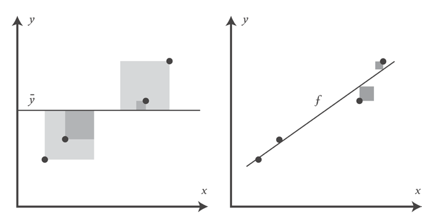
Левый график показывает дисперсию модели, которая всегда угадывает среднее значение для , правый же показывает меньшие по размеру квадраты, связанные с остатками, которые остались необъясненными моделью f. С чисто геометрической точки зрения можно увидеть, как модель объяснила большинство дисперсии в y. Приведенный ниже пример вычисляет R2 путем деления дисперсии остатков на дисперсию значений y:
def r_squared(a, b, xs, ys):
'''Рассчитать коэффициент детерминации (R-квадрат)'''
r_var = residuals(a, b, xs, ys).var()
y_var = ys.var()
return 1 - (r_var / y_var)
def ex_3_15():
'''Рассчитать коэффициент R-квадрат
на примере данных роста и веса'''
df = swimmer_data()
X = df['Рост, см'].apply( jitter(0.5) )
y = df['Вес'].apply(np.log)
a, b = intercept(X, y), slope(X, y)
return r_squared(a, b, X, y)
0.75268223613272323
В результате получим значение 0.753. Другими словами, более 75% дисперсии веса пловцов, выступавших на Олимпийских играх 2012 г., можно объяснить ростом.
В случае простой регрессионной модели (с одной независимой переменной), связь между коэффициентом детерминации R2 и коэффициентом корреляции r является прямолинейной:
Коэффициент корреляции r может означать, что половина изменчивости в переменной Y объясняется переменной X, но фактически R2 составит 0.52, т.е. 0.25.
Множественная линейная регрессия
Пока что в этой серии постов мы видели, как строится линия регрессии с одной независимой переменной. Однако, нередко желательно построить модель с несколькими независимыми переменными. Такая модель называется множественной линейной регрессией.Каждой независимой переменной потребуется свой собственный коэффициент. Вместо того, чтобы для каждой из них пытаться подобрать букву в алфавите, зададим новую переменную β (бета), которая будет содержать все наши коэффициенты:
Такая модель эквивалентна двухфакторной линейно-регрессионной модели, где β1 = a и β2 = b при условии, что x1 всегда гарантированно равен 1, вследствие чего β1 — это всегда константная составляющая, которая представляет наше пересечение, при этом x1 называется постоянным смещением уравнения регрессии, или членом смещения.
Обобщив линейное уравнение в терминах β, его легко расширить на столько коэффициентов, насколько нам нужно:
Каждое значение от x1 до xn соответствует независимой переменной, которая могла бы объяснить значение y. Каждое значение от β1 до βn соответствует коэффициенту, который устанавливает относительный вклад независимой переменной.
Простая линейная регрессия преследовала цель объяснить вес исключительно с точки зрения роста, однако объяснить вес людей помогает много других факторов: их возраст, пол, питание, тип телосложения. Мы располагаем сведениями о возрасте олимпийских пловцов, поэтому мы смогли бы построить модель, которая учитывает и эти дополнительные данные.
До настоящего момента мы предоставляли независимую переменную в виде одной последовательности значений, однако при наличии двух и более параметров нам нужно предоставлять несколько значений для каждого x. Мы можем воспользоваться функциональностью библиотеки pandas, чтобы выбрать два и более столбцов и управлять каждым как списком, но есть способ получше: матрицы.
Темой следующего поста, поста №3, будут матричные операции, нормальное уравнение и коллинеарность.
Источник статьи: https://habr.com/ru/post/558084/
